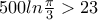
Δίνεται..
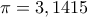
Συντονιστής: Παύλος Μαραγκουδάκης
Θα χρησιμοποιήσουμε τιςΛάμπρος Μπαλός έγραψε:Δείξτε ότι :
Δίνεται..

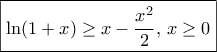 .
. 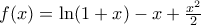 τότε
τότε  (αύξουσα). Άρα για
(αύξουσα). Άρα για  έχουμε
έχουμε  , που ισοδυναμεί με το αποδεικτέο.
, που ισοδυναμεί με το αποδεικτέο.
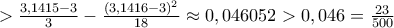 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες