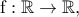 για την οποία ισχύει
για την οποία ισχύει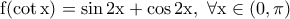
και η συνάρτηση
 με
με 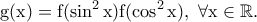
Να βρεθούν οι άκρες τιμές της συνάρτησης

Viet Nam.
Συντονιστής: Παύλος Μαραγκουδάκης
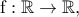 για την οποία ισχύει
για την οποία ισχύει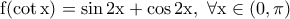
 με
με 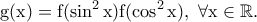

Εστω
 . Επίσης
. Επίσης
 .
. . Ομοίως και για το
. Ομοίως και για το  . Επομένως μια θεωρητικά ελάχιστη τιμή της
. Επομένως μια θεωρητικά ελάχιστη τιμή της  είναι το
είναι το  το οποίο επαληθεύεται όταν
το οποίο επαληθεύεται όταν 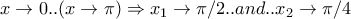 .
. θα την αντιμετωπίσουμε ως συνάρτηση δύο μεταβλητών με περιορισμό. Συγκεκριμένα ζητάμε:
θα την αντιμετωπίσουμε ως συνάρτηση δύο μεταβλητών με περιορισμό. Συγκεκριμένα ζητάμε:![max\left \{ g(x_{1},x_{2}) \right \}=max\left \{\left [ sin(2x_{1})+cos(2x_{1}) \right ] *\left [ sin(2x_{2})+cos(2x_{2}) \right ]\right \} max\left \{ g(x_{1},x_{2}) \right \}=max\left \{\left [ sin(2x_{1})+cos(2x_{1}) \right ] *\left [ sin(2x_{2})+cos(2x_{2}) \right ]\right \}](/forum/ext/geomar/texintegr/latexrender/pictures/84b833ef27cad6a9b6bb1b1090609e23.png)
 .
.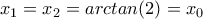

 .
. .
.![g(x)\in (-1,0.04] g(x)\in (-1,0.04]](/forum/ext/geomar/texintegr/latexrender/pictures/92747aac6181ebc0c0692f86a7046425.png)
 , οπότε :
, οπότε :  , δηλαδή :
, δηλαδή : 
 , τουτέστιν :
, τουτέστιν :  και :
και : 
 .
.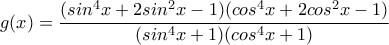 .
.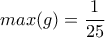 , π.χ για :
, π.χ για : 
 , π.χ για :
, π.χ για : 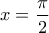 (τα τελευταία με λογισμικό
(τα τελευταία με λογισμικό Με συγχωρείτε, μα αυτά ανοίκουν σε ανοικτό διάστημα. Οι τιμές αυτές δεν πιάνονται.
Για το μέγιστο, ας δούμε και μια αναλυτική προσέγγιση της μεθόδου με πολλαπλασιαστές Lagrange:
![g(x_1,x_2)=[\sin(2x_1)+\cos(2x_1)][\sin(2x_2)+\cos(2x_2)] g(x_1,x_2)=[\sin(2x_1)+\cos(2x_1)][\sin(2x_2)+\cos(2x_2)]](/forum/ext/geomar/texintegr/latexrender/pictures/f8ac0248d45c8ad3c0aec9a86ea18a3d.png) , με
, με  μια συνάρτηση περιορισμού.
μια συνάρτηση περιορισμού. είναι συνεχείς συναρτήσεις με συνεχείς μερικές παραγώγους.
είναι συνεχείς συναρτήσεις με συνεχείς μερικές παραγώγους. όταν η κλίση της
όταν η κλίση της  μηδενίζεται.
μηδενίζεται.![\bigtriangledown h=\begin{bmatrix} \dfrac{\partial }{\partial x_1}\\\ \dfrac{\partial }{\partial x_2} \end{bmatrix}= \begin{bmatrix} [\sin(2x_2)+\cos(2x_2)][2(\cos(2x_1)-\sin(2x_1))]\\\ [\sin(2x_1)+\cos(2x_1)][2(\cos(2x_2)-\sin(2x_2))] \end{bmatrix}=0 \bigtriangledown h=\begin{bmatrix} \dfrac{\partial }{\partial x_1}\\\ \dfrac{\partial }{\partial x_2} \end{bmatrix}= \begin{bmatrix} [\sin(2x_2)+\cos(2x_2)][2(\cos(2x_1)-\sin(2x_1))]\\\ [\sin(2x_1)+\cos(2x_1)][2(\cos(2x_2)-\sin(2x_2))] \end{bmatrix}=0](/forum/ext/geomar/texintegr/latexrender/pictures/f82d44032896cf70c7eb3fbd6448dad6.png)
 .
. , που επιτυγχάνεται όταν
, που επιτυγχάνεται όταν 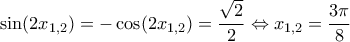 και μόνο τότε, κάτι που μπορεί εύκολα να αποδειχθεί εξετάζοντας την μονοτονία της
και μόνο τότε, κάτι που μπορεί εύκολα να αποδειχθεί εξετάζοντας την μονοτονία της  στο συγκεκριμένο διάστημα.
στο συγκεκριμένο διάστημα. , αποκλείεται μέγιστο.
, αποκλείεται μέγιστο. ,
,  είναι ανοικτό, οπότε ονομάζουμε
είναι ανοικτό, οπότε ονομάζουμε ![\bar{U}=[\dfrac{\pi}{4},\dfrac{\pi}{2}]^{2} \bar{U}=[\dfrac{\pi}{4},\dfrac{\pi}{2}]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/f07c572baf911951792b5dc761ce16b7.png) το κλείσιμο του
το κλείσιμο του  . Τότε, το σύνολο
. Τότε, το σύνολο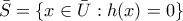
 παρουσιάζει μέγιστο στο
παρουσιάζει μέγιστο στο  , ας πούμε το
, ας πούμε το  .
. , ας πούμε χωρίς βλάβη της γενικότητας το
, ας πούμε χωρίς βλάβη της γενικότητας το  να βρίσκεται στο
να βρίσκεται στο  . Τότε, χρησιμοποιόντας και την συνθήκη παίρνουμε
. Τότε, χρησιμοποιόντας και την συνθήκη παίρνουμε  και για την
και για την  παίρνουμε
παίρνουμε  , αποκλείεται μέγιστο
, αποκλείεται μέγιστο να βρίσκεται στο
να βρίσκεται στο  . Τότε, οι πολλαπλασιαστές Lagrange δίνουν:
. Τότε, οι πολλαπλασιαστές Lagrange δίνουν:![\bigtriangledown g=\lambda \bigtriangledown h\Leftrightarrow \begin{bmatrix} [\sin(2x_2)+\cos(2x_2)][2(\cos(2x_1)-\sin(2x_1))]\\\ [\sin(2x_1)+\cos(2x_1)][2(\cos(2x_2)-\sin(2x_2))] \end{bmatrix}=\lambda \begin{bmatrix} -\csc^{2}x_1\\ -\csc^{2}x_2 \end{bmatrix} \bigtriangledown g=\lambda \bigtriangledown h\Leftrightarrow \begin{bmatrix} [\sin(2x_2)+\cos(2x_2)][2(\cos(2x_1)-\sin(2x_1))]\\\ [\sin(2x_1)+\cos(2x_1)][2(\cos(2x_2)-\sin(2x_2))] \end{bmatrix}=\lambda \begin{bmatrix} -\csc^{2}x_1\\ -\csc^{2}x_2 \end{bmatrix}](/forum/ext/geomar/texintegr/latexrender/pictures/0459c46f05cc3dce00d39ffa2621ed71.png)
![\begin{cases}[\sin(2x_2)+\cos(2x_2)][2(\cos(2x_1)-\sin(2x_1))]=\lambda (-\csc^{2}x_1) \\ [\sin(2x_1)+\cos(2x_1)][2(\cos(2x_2)-\sin(2x_2))]=\lambda (-\csc^{2}x_2) \end{cases}\Rightarrow \begin{cases}[\sin(2x_2)+\cos(2x_2)][2(\cos(2x_1)-\sin(2x_1))]=\lambda (-\csc^{2}x_1) \\ [\sin(2x_1)+\cos(2x_1)][2(\cos(2x_2)-\sin(2x_2))]=\lambda (-\csc^{2}x_2) \end{cases}\Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/2b657a45b7392a64790884cbea6e892f.png)
![\Rightarrow \dfrac{[sin(2x_2)+cos(2x_2)][2(cos(2x_1)-sin(2x_1))]}{\csc^{2}x_1}=\dfrac{[sin(2x_1)+cos(2x_1)][2(cos(2x_2)-sin(2x_2))]}{\csc^{2}x_2} \Rightarrow \dfrac{[sin(2x_2)+cos(2x_2)][2(cos(2x_1)-sin(2x_1))]}{\csc^{2}x_1}=\dfrac{[sin(2x_1)+cos(2x_1)][2(cos(2x_2)-sin(2x_2))]}{\csc^{2}x_2}](/forum/ext/geomar/texintegr/latexrender/pictures/dfdc41faec9172a9ebf40fa211584a9a.png)
 , αλλά είναι η μόνη; Ένα λογισμικό ίσως να βοηθούσε εδώ.
, αλλά είναι η μόνη; Ένα λογισμικό ίσως να βοηθούσε εδώ.Μόλις διαπίστωσα ένα λάθος σε αυτό το μέρος. Η κλίση αυτή είναι τηςthepigod762 έγραψε: ↑Κυρ Ιαν 16, 2022 9:39 pmΓια το μέγιστο, ας δούμε και μια αναλυτική προσέγγιση της μεθόδου με πολλαπλασιαστές Lagrange:
Θέλουμε να μεγιστοποιήσουμε την, με
μια συνάρτηση περιορισμού.
Οιείναι συνεχείς συναρτήσεις με συνεχείς μερικές παραγώγους.
Αρχικά θα εξετάσουμε τις τιμές τηςόταν η κλίση της
μηδενίζεται.
Τότε θα είναι
Εύκολα βλέπουμε ότι.
Επομένως πρέπει να είναι
, που επιτυγχάνεται όταν
και μόνο τότε, κάτι που μπορεί εύκολα να αποδειχθεί εξετάζοντας την μονοτονία της
στο συγκεκριμένο διάστημα.
Τότε, θα είναι, αποκλείεται μέγιστο.
 και όχι της
και όχι της  ! Έτσι, αυτή η περίπτωση δεν χρειάζεται καν, αφού τώρα παρατηρούμε ότι η κλίση είναι αδύνατο να μηδενιστεί.
! Έτσι, αυτή η περίπτωση δεν χρειάζεται καν, αφού τώρα παρατηρούμε ότι η κλίση είναι αδύνατο να μηδενιστεί. 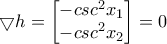 , που είναι αδύνατο.
, που είναι αδύνατο.Με τη βοήθεια των τριγωνομετρικών τύπων δείχνουμε, όπως έκανε παραπάνω ο Θανάσης, ότι:

![\displaystyle h(x)=f(x)f(1-x), \ \ x\in[0,1] \displaystyle h(x)=f(x)f(1-x), \ \ x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/71d9ff8c4c57152f79d7154eb3645999.png)
 ισχύουν τα παρακάτω:
ισχύουν τα παρακάτω:
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle [0,1] \displaystyle [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/7776f97d313473b00efd738476715d92.png) , με σύνολο τιμών το
, με σύνολο τιμών το ![\displaystyle [-1,1] \displaystyle [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d5f3625362b404389aedaac05aa34f50.png)
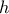 είναι το
είναι το  , για
, για  , ή
, ή 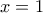 .
.![\displaystyle h^{\prime}(x)=f^{\prime}(x)f(1-x)-f^{\prime}(1-x)f(x), x \in[0,1] \displaystyle h^{\prime}(x)=f^{\prime}(x)f(1-x)-f^{\prime}(1-x)f(x), x \in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5e70c99479e93606745d886028d007e2.png)
 είναι ο αριθμός
είναι ο αριθμός  .
.  , και αφού
, και αφού  θα είναι:
θα είναι: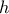 γνησίως αύξουσα στο
γνησίως αύξουσα στο ![\displaystyle \left[0,\frac{1}{2}\right] \displaystyle \left[0,\frac{1}{2}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/739ce2e4423182d1781f1698f5a86542.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![\displaystyle \left[\frac{1}{2},1\right] \displaystyle \left[\frac{1}{2},1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/e69d931b586c39d9f23d71c26640b80f.png)
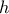 είναι ο αριθμός
είναι ο αριθμός  .
. στα οποία η συνάρτηση
στα οποία η συνάρτηση  έχει ελάχιστο, μέγιστο επιλύουμε τις εξισώσεις:
έχει ελάχιστο, μέγιστο επιλύουμε τις εξισώσεις:  ή
ή 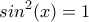 για το ελάχιστο
για το ελάχιστο  για το μέγιστο.
για το μέγιστο.  παρουσιάζονται στα σημεία
παρουσιάζονται στα σημεία 


abgd έγραψε: ↑Δευ Ιαν 17, 2022 2:39 pmΜε τη βοήθεια των τριγωνομετρικών τύπων δείχνουμε, όπως έκανε παραπάνω ο Θανάσης, ότι:
Το πρόβλημα είναι ισοδύναμο με την εύρεση των ακροτάτων της συνάρτησης
Για την συνάρτησηισχύουν τα παρακάτω:
Η συνάρτησηείναι γνησίως αύξουσα στο
, με σύνολο τιμών το
Εύκολα, συνεπώς, μπορούμε να δικαιολογήσουμε ότι η ελάχιστη τιμή τηςείναι το
, για
, ή
.
Ακόμη,
Μία προφανής ρίζα τηςείναι ο αριθμός
.
Μπορούμε τώρα να δείξουμε ότι δεν έχουμε άλλη ρίζα, με τη βοήθεια της συνάρτησης, και αφού
θα είναι:
γνησίως αύξουσα στο
και γνησίως φθίνουσα στο
Έτσι, η μέγιστη τιμή τηςείναι ο αριθμός
.
Για την εύρεση τωνστα οποία η συνάρτηση
έχει ελάχιστο, μέγιστο επιλύουμε τις εξισώσεις:
ή
για το ελάχιστο
και τηνγια το μέγιστο.
Παρατηρούμε ότι τα ακρότατα τηςπαρουσιάζονται στα σημεία

 είναι ο αριθμός
είναι ο αριθμός  .
. Γιατί όχι;ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Ιαν 17, 2022 3:33 pmΔεν νομίζω ότι το
Μπορούμε τώρα να δείξουμε ότι δεν έχουμε άλλη ρίζα
ισχύει .
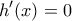 είναι ισοδύναμη με την
είναι ισοδύναμη με την  .
.
 οπότε
οπότε  γνησίως αύξουσα και
γνησίως αύξουσα και  γνησίως φθίνουσα με το ίδιο σύνολο τιμών το
γνησίως φθίνουσα με το ίδιο σύνολο τιμών το ![\displaystyle [-\frac{1}{2},1] \displaystyle [-\frac{1}{2},1]](/forum/ext/geomar/texintegr/latexrender/pictures/867dedec891ae2629307993539fa7528.png) . Το ζητούμενο έπεται εύκολα, (Bolzano, μονοτονία για την
. Το ζητούμενο έπεται εύκολα, (Bolzano, μονοτονία για την  ).
).

Εχετε δίκιο.abgd έγραψε: ↑Δευ Ιαν 17, 2022 4:38 pmΓιατί όχι;ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Ιαν 17, 2022 3:33 pmΔεν νομίζω ότι το
Μπορούμε τώρα να δείξουμε ότι δεν έχουμε άλλη ρίζα
ισχύει .
Πιο αναλυτικά:
Η εξίσωσηείναι ισοδύναμη με την
.
Θεωρούμε τις συναρτήσεις:
Είναι:
οπότε
γνησίως αύξουσα και
γνησίως φθίνουσα με το ίδιο σύνολο τιμών το
. Το ζητούμενο έπεται εύκολα, (Bolzano, μονοτονία για την
).
 .
. .
. .
. .
. , διότι ισοδυναμεί με
, διότι ισοδυναμεί με  , που ισχύει.
, που ισχύει. .
.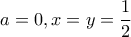 .
. .
. .
. , διότι
, διότι  .
. , που ισχύει.
, που ισχύει. , με ισότητα για
, με ισότητα για  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες