 είναι ορθογώνιο και ισοσκελές . Σημείο
είναι ορθογώνιο και ισοσκελές . Σημείο  κινείται στο εσωτερικό του
κινείται στο εσωτερικό τουτεταρτοκυκλίου
 . Βρείτε τη θέση του
. Βρείτε τη θέση του  η οποία μεγιστοποιεί τη διαφορά :
η οποία μεγιστοποιεί τη διαφορά :  .
.Συντονιστής: Παύλος Μαραγκουδάκης
 είναι ορθογώνιο και ισοσκελές . Σημείο
είναι ορθογώνιο και ισοσκελές . Σημείο  κινείται στο εσωτερικό του
κινείται στο εσωτερικό του . Βρείτε τη θέση του
. Βρείτε τη θέση του  η οποία μεγιστοποιεί τη διαφορά :
η οποία μεγιστοποιεί τη διαφορά :  .
.Φέρω το ύψος
 από το
από το  προς την
προς την  . Εύκολα
. Εύκολα  και
και  . Θα υποθέσω, επιπλέον, χωρίς βλάβη της γενικότητας πως
. Θα υποθέσω, επιπλέον, χωρίς βλάβη της γενικότητας πως  .
.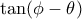 . Είναι:
. Είναι: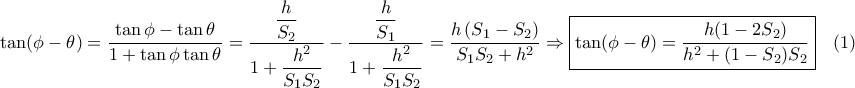
 ανήκει στο τόξο
ανήκει στο τόξο  , οπότε ισχύει επίσης:
, οπότε ισχύει επίσης:
 . Και έτσι παίρνω:
. Και έτσι παίρνω: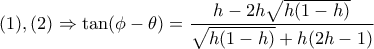
 και λαμβάνεται όταν
και λαμβάνεται όταν 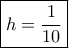 . Για
. Για  ,
,  .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες