(α) Να δειχθεί ότι οι εφαπτόμενες από τα σημεία
 στον μοναδιαίο κύκλο
στον μοναδιαίο κύκλο 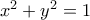 γεννούν τις Πυθαγόρειες Τριάδες
γεννούν τις Πυθαγόρειες Τριάδες  .
.(b)* Γενικεύστε και σχολιάστε όσο και όπως μπορείτε.
Συντονιστής: Παύλος Μαραγκουδάκης
 στον μοναδιαίο κύκλο
στον μοναδιαίο κύκλο 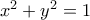 γεννούν τις Πυθαγόρειες Τριάδες
γεννούν τις Πυθαγόρειες Τριάδες  .
.Γιώργο, αυτό ζητάς:
 τυχαίο σημείο του κύκλου, δηλαδή ισχύει
τυχαίο σημείο του κύκλου, δηλαδή ισχύει  . H κλίση της ακτίνας που συνδέει το κέντρο
. H κλίση της ακτίνας που συνδέει το κέντρο  με το
με το  είναι
είναι  , οπότε η εφαπτομένη στο
, οπότε η εφαπτομένη στο  η οποία διέρχεται από το
η οποία διέρχεται από το  είναι η
είναι η .
.  βρίσκεται στην εν λόγω εφαπτομένη, έχουμε
βρίσκεται στην εν λόγω εφαπτομένη, έχουμε  ή αλλιώς
ή αλλιώς , που σημαίνει
, που σημαίνει  . Θέτουμε αυτό το
. Θέτουμε αυτό το  στην αρχική, οπότε
στην αρχική, οπότε  . Με απλοποίηση δίνει
. Με απλοποίηση δίνει  από όπου αμέσως
από όπου αμέσως 
 γράφεται
γράφεται  ή αλλιώς
ή αλλιώς  (βρήκαμε δηλαδή Πυθαγόρειες τριάδες)
(βρήκαμε δηλαδή Πυθαγόρειες τριάδες) σημείο του κύκλου με ρητές συντεταγμένες, η παραπάνω διαδικασία με ανάποδη σειρά δείχνει ότι η εφαπτομένη στο
σημείο του κύκλου με ρητές συντεταγμένες, η παραπάνω διαδικασία με ανάποδη σειρά δείχνει ότι η εφαπτομένη στο  τέμνει την
τέμνει την  σε ρητό σημείο
σε ρητό σημείο  .
. . Προφανώς :
. Προφανώς :  , που σημαίνει ότι το
, που σημαίνει ότι το  είναι σημείο του κύκλου :
είναι σημείο του κύκλου : 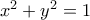 .
. του
του  , βρίσκονται με χρήση του τύπου :
, βρίσκονται με χρήση του τύπου :  ,
, .
.Γεια σας. Γιώργο γράφω κάποια σχόλια που στηρίζονται σε γνωστά πράγματα. Ας θέσουμε
 . Αν ονoμάσουμε
. Αν ονoμάσουμε  το σημείο
το σημείο  τότε η
τότε η  είναι η πολική του
είναι η πολική του  ως προς τον κύκλο και έχει εξίσωση
ως προς τον κύκλο και έχει εξίσωση  δηλαδη
δηλαδη  . Επειδή έχει ήδη ένα κοινό σημείο με τον κύκλο, το
. Επειδή έχει ήδη ένα κοινό σημείο με τον κύκλο, το  , το δεύτερο κοινό σημείο
, το δεύτερο κοινό σημείο  βρίσκεται χρησιμοπιώντας μόνο τις 4 πράξεις και επομένως είναι ρητό σημείο. Με αυτό τον τρόπο βρίσκουμε όλα τα ρητά σημεία του κύλου και από αυτά εκείνα με ακέραιες συντεταγμένες. Η γενική ιδέα είναι η ακόλουθη:
βρίσκεται χρησιμοπιώντας μόνο τις 4 πράξεις και επομένως είναι ρητό σημείο. Με αυτό τον τρόπο βρίσκουμε όλα τα ρητά σημεία του κύλου και από αυτά εκείνα με ακέραιες συντεταγμένες. Η γενική ιδέα είναι η ακόλουθη: με ακέραιους συντελεστές και είμαστε σε θέση να βρούμε ένα ρητό σημείο της
με ακέραιους συντελεστές και είμαστε σε θέση να βρούμε ένα ρητό σημείο της  (εδώ είναι ο κύκλος και το
(εδώ είναι ο κύκλος και το  ) τότε θεωρούμε μία μεταβλητή ευθεία
) τότε θεωρούμε μία μεταβλητή ευθεία  . Οι συντεταγμένες του δεύτερου σημείο τομής της με την κωνική είναι πάντα ρητές εκφράσεις των
. Οι συντεταγμένες του δεύτερου σημείο τομής της με την κωνική είναι πάντα ρητές εκφράσεις των  ,
,  ,
,  . Αν το
. Αν το  είναι ρητός αριθμός είναι και αυτές ρητοί. Αντιστρόφως αν είναι ρητοί αριθμοί τότε και ο συντελεστής διευθύνσεως της ευθείας που συνδέει τα δύο σημεία τομής θα είναι ρητός. Επομένως η εξίσωση
είναι ρητός αριθμός είναι και αυτές ρητοί. Αντιστρόφως αν είναι ρητοί αριθμοί τότε και ο συντελεστής διευθύνσεως της ευθείας που συνδέει τα δύο σημεία τομής θα είναι ρητός. Επομένως η εξίσωση  μας οδηγεί σε όλα τα ρητά σημεία της κωνικής (εδώ το
μας οδηγεί σε όλα τα ρητά σημεία της κωνικής (εδώ το  είναι το
είναι το  ).
).Θανάση η αλήθεια είναι ότι δεν αναρτήθηκε το σχήμα στην αρχική δημοσίευση της 31-12-21, αλλά προστέθηκε στις 8-1-22 (όταν συνόδευσε σχετική δημοσίευση στο ΦΒ δηλαδή). Στον αντίποδα τώρα, φαίνεται ότι το ερώτημα δεν ήταν κατανοητό όπως τέθηκε, γι αυτό και παρέμεινε αναπάντητο ως τις 10-1-22!KARKAR έγραψε: ↑Δευ Ιαν 10, 2022 8:03 pmΠυθαγόρειες τριάδες.pngΓιώργο δεν κατάλαβα ποιο είναι το ερώτημα , αφού δίνεις τις συντεταγμένες του. Προφανώς :
, που σημαίνει ότι το
είναι σημείο του κύκλου :
.
Οι συντεταγμένεςτου
, βρίσκονται με χρήση του τύπου :
,
αξιοποιώντας την πληροφορία ότι η εφαπτομένη διέρχεται από το σημείο :.
Ενόσω έγραφα , αναρτήθηκε παρόμοια ανάρτηση από τον Μιχάλη . Το αφήνω ... πιο πολύ για το σχήμα .
 και
και  . (Ας παρατηρηθεί με την ευκαιρία ότι η προσέγγιση αυτή, που βασίζεται στην ισότητα των μηκών των εφαπτομένων, μπορεί επίσης να χρησιμοποιηθεί για να υπολογισθεί η κλίση της εφαπτομένης στο τυχόν σημείο
. (Ας παρατηρηθεί με την ευκαιρία ότι η προσέγγιση αυτή, που βασίζεται στην ισότητα των μηκών των εφαπτομένων, μπορεί επίσης να χρησιμοποιηθεί για να υπολογισθεί η κλίση της εφαπτομένης στο τυχόν σημείο  του κύκλου χωρίς χρήση Λογισμού ή/και για να 'επαληθευθεί' η τιμή που μας δίνει η παράγωγος.)
του κύκλου χωρίς χρήση Λογισμού ή/και για να 'επαληθευθεί' η τιμή που μας δίνει η παράγωγος.)gbaloglou έγραψε: ↑Τετ Ιαν 12, 2022 12:26 pmΘανάση η αλήθεια είναι ότι δεν αναρτήθηκε το σχήμα στην αρχική δημοσίευση της 31-12-21, αλλά προστέθηκε στις 8-1-22 (όταν συνόδευσε σχετική δημοσίευση στο ΦΒ δηλαδή). Στον αντίποδα τώρα, φαίνεται ότι το ερώτημα δεν ήταν κατανοητό όπως τέθηκε, γι αυτό και παρέμεινε αναπάντητο ως τις 10-1-22!KARKAR έγραψε: ↑Δευ Ιαν 10, 2022 8:03 pmΠυθαγόρειες τριάδες.pngΓιώργο δεν κατάλαβα ποιο είναι το ερώτημα , αφού δίνεις τις συντεταγμένες του. Προφανώς :
, που σημαίνει ότι το
είναι σημείο του κύκλου :
.
Οι συντεταγμένεςτου
, βρίσκονται με χρήση του τύπου :
,
αξιοποιώντας την πληροφορία ότι η εφαπτομένη διέρχεται από το σημείο :.
Ενόσω έγραφα , αναρτήθηκε παρόμοια ανάρτηση από τον Μιχάλη . Το αφήνω ... πιο πολύ για το σχήμα .
Η εύκολα αποδεικνυόμενη αλλά ιδιαίτερα όμορφη και μάλλον αναπάντεχη αυτή ιδιότητα της εφαπτομένης φαίνεται να είναι άγνωστη. Για γενικεύσεις λίγο χλωμό το βλέπω. (Το πολύ ενδιαφέρον αποτέλεσμα για ρητά ελλειπτικά σημεία που παραθέτει ο Νίκος πάει σε άλλη κατεύθυνση, καθώς δεν αφορά εφαπτόμενες αλλά τέμνουσες.)
Γεια σαςgbaloglou έγραψε: ↑Τετ Ιαν 12, 2022 12:26 pmΗ εύκολα αποδεικνυόμενη αλλά ιδιαίτερα όμορφη και μάλλον αναπάντεχη αυτή ιδιότητα της εφαπτομένης φαίνεται να είναι άγνωστη. Για γενικεύσεις λίγο χλωμό το βλέπω. (Το πολύ ενδιαφέρον αποτέλεσμα για ρητά ελλειπτικά σημεία που παραθέτει ο Νίκος πάει σε άλλη κατεύθυνση, καθώς δεν αφορά εφαπτόμενες αλλά τέμνουσες.)
 ,
, 
 ακεραίους. Έστω
ακεραίους. Έστω 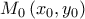 ένα σημείο της με ρητές συντεταγμένες και
ένα σημείο της με ρητές συντεταγμένες και  η εφαπτομένη της
η εφαπτομένη της  στο
στο  . Σε κάθε σημείο
. Σε κάθε σημείο  της
της  διάφορο του
διάφορο του  αντιστοιχούμε το σημείο επαφής
αντιστοιχούμε το σημείο επαφής  της εφαπτομένης που άγεται από αυτό προς την κωνική και είναι διάφορη της
της εφαπτομένης που άγεται από αυτό προς την κωνική και είναι διάφορη της  . Τότε η αντιστοιχία
. Τότε η αντιστοιχία  αντιιστοιχίζει ρητά σημεία της
αντιιστοιχίζει ρητά σημεία της  σε ρητά σημεία της
σε ρητά σημεία της  .
. τότε οι εξισώσεις των εφαπτομένων στα
τότε οι εξισώσεις των εφαπτομένων στα  ,
,  είναι:
είναι:

 .
H εξίσωση:
.
H εξίσωση:  .
.
 .
.  διότι αυτό δεν ανήκει στην κωνική.
διότι αυτό δεν ανήκει στην κωνική.  .
. είναι λύση του συστήματος:
είναι λύση του συστήματος:
 .
. και επιλύεται τουλάχιστον ως προς ένα από τους αγνώσττους
και επιλύεται τουλάχιστον ως προς ένα από τους αγνώσττους  . Σε κάθε περίπτωση ο άγνωστος ως προς τον οποίο θα επιλυθεί είναι ρητή συνάρτηση του άλλου με ρητούς συντελεστές. Επομένως όταν αντικατασταθεί στην πρώτη εξίσωση θα μας δώσει μια δευτεροβάθμια εξίσωση ως προς τον άλλο άγνωστο της οποίας οι συντελεστές και μία ρίζα (η
. Σε κάθε περίπτωση ο άγνωστος ως προς τον οποίο θα επιλυθεί είναι ρητή συνάρτηση του άλλου με ρητούς συντελεστές. Επομένως όταν αντικατασταθεί στην πρώτη εξίσωση θα μας δώσει μια δευτεροβάθμια εξίσωση ως προς τον άλλο άγνωστο της οποίας οι συντελεστές και μία ρίζα (η  ή η
ή η  ανάλογα με το αν επιλύσαμε ως προς
ανάλογα με το αν επιλύσαμε ως προς  ή
ή  ) είναι ρητοί αριθμοί. Επομένως και η άλλη ρίζα είναι ρητή. Συμπεραίνουμε έτσι ότι τα
) είναι ρητοί αριθμοί. Επομένως και η άλλη ρίζα είναι ρητή. Συμπεραίνουμε έτσι ότι τα  ,
,  είναι ρητοί.
είναι ρητοί.Γιώργο, η λύση που έγραψα δεν χρησιμοποιεί Λογισμό. Χρησιμοποιεί το γεγονός (που ως γνωστόν υπάρχει στα Στοιχεία του Ευκλείδη) ότι η εφαπτομένη είναι κάθετη στο άκρο της αντίστοιχης ακτίνας.
Μιχάλη όντως, είδα το λάθος μου αρκετές ώρες πριν στείλεις την παραπάνω δημοσίευση (#8) ... και νόμισα ότι έσβησα την δεύτερη παράγραφο της δικής μου δημοσίευσης (#5), προς μεγάλη μου όμως έκπληξη την βλέπω ακόμη εκεί ... οπότε και την αφήνω ως έχει. [Τώρα βλέπω τι συνέβη: αντί απλώς να σβήσω την δεύτερη παράγραφο στην δημοσίευση #5 δημιούργησα νέα δημοσίευση (#6) χωρίς αυτήν την δεύτερη παράγραφο!Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 13, 2022 1:59 amΓιώργο, η λύση που έγραψα δεν χρησιμοποιεί Λογισμό. Χρησιμοποιεί το γεγονός (που ως γνωστόν υπάρχει στα Στοιχεία του Ευκλείδη) ότι η εφαπτομένη είναι κάθετη στο άκρο της αντίστοιχης ακτίνας.
Νίκο πολύ εύστοχα τα παραπάνω, που στην ειδική περίπτωση του κύκλου λαμβάνουν την εξής 'συγκεκριμένη' μορφή:nsmavrogiannis έγραψε: ↑Πέμ Ιαν 13, 2022 1:45 amΓεια σαςgbaloglou έγραψε: ↑Τετ Ιαν 12, 2022 12:26 pmΗ εύκολα αποδεικνυόμενη αλλά ιδιαίτερα όμορφη και μάλλον αναπάντεχη αυτή ιδιότητα της εφαπτομένης φαίνεται να είναι άγνωστη. Για γενικεύσεις λίγο χλωμό το βλέπω. (Το πολύ ενδιαφέρον αποτέλεσμα για ρητά ελλειπτικά σημεία που παραθέτει ο Νίκος πάει σε άλλη κατεύθυνση, καθώς δεν αφορά εφαπτόμενες αλλά τέμνουσες.)
Γιώργο νομίζω ότι υπάρχει μια σύνδεση και η διαδικασία που έχεις βρει γενικεύεται. Γράφω κάπως πιο αναλυτικά.
Θα αποδείξουμε το ακόλουθο:
Έστω μια μη εκφυλισμένη κωνική
,
με ταακεραίους. Έστω
ένα σημείο της με ρητές συντεταγμένες και
η εφαπτομένη της
στο
. Σε κάθε σημείο
της
διάφορο του
αντιστοιχούμε το σημείο επαφής
της εφαπτομένης που άγεται από αυτό προς την κωνική και είναι διάφορη της
. Τότε η αντιστοιχία
αντιιστοιχίζει ρητά σημεία της
σε ρητά σημεία της
.
Πράγματι αν είναιτότε οι εξισώσεις των εφαπτομένων στα
,
είναι:
και φυσικά επαληθεύονται από το.
rationalpoints.png
H εξίσωση:
.
α) είναι της μορφής
β) επαληθεύεται από δύο σημεία τα.
γ) δεν επαληθεύεται από τοδιότι αυτό δεν ανήκει στην κωνική.
Άρα πρόκειται για εξίσωση ευθείας και συγκεκριμένα της.
Άρα τοείναι λύση του συστήματος:
το οποίο έχει το πολύ δύο λύσεις εκ των οποίων η μία είναι ήδη η.
Η δεύτερη εξίσωση του συστήματος γράφεται
και επιλύεται τουλάχιστον ως προς ένα από τους αγνώσττους
. Σε κάθε περίπτωση ο άγνωστος ως προς τον οποίο θα επιλυθεί είναι ρητή συνάρτηση του άλλου με ρητούς συντελεστές. Επομένως όταν αντικατασταθεί στην πρώτη εξίσωση θα μας δώσει μια δευτεροβάθμια εξίσωση ως προς τον άλλο άγνωστο της οποίας οι συντελεστές και μία ρίζα (η
ή η
ανάλογα με το αν επιλύσαμε ως προς
ή
) είναι ρητοί αριθμοί. Επομένως και η άλλη ρίζα είναι ρητή. Συμπεραίνουμε έτσι ότι τα
,
είναι ρητοί.
 είναι ρητό σημείο επαφής του κύκλου
είναι ρητό σημείο επαφής του κύκλου 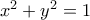 και της εφαπτομένης που άγεται από το επίσης ρητό σημείο
και της εφαπτομένης που άγεται από το επίσης ρητό σημείο  τότε το σημείο επαφής της άλλης εφαπτομένης είναι επίσης ρητό και οι συντεταγμένες του δίνονται από τον τύπο
τότε το σημείο επαφής της άλλης εφαπτομένης είναι επίσης ρητό και οι συντεταγμένες του δίνονται από τον τύπο
 . Από τους τέσσερις δυνατούς συνδυασμούς των συν-πλην είναι αποδεκτοί μόνον οι δύο, και ο ένας από αυτούς τους δύο μας 'επιστρέφει' το αρχικό σημείο επαφής,
. Από τους τέσσερις δυνατούς συνδυασμούς των συν-πλην είναι αποδεκτοί μόνον οι δύο, και ο ένας από αυτούς τους δύο μας 'επιστρέφει' το αρχικό σημείο επαφής,  .
. ,
, 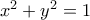 .)]
.)]Μέλη σε αυτήν τη Δ. Συζήτηση: gbaloglou και 6 επισκέπτες