Η τυπική απόκλιση ισούται με
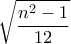
(απλό). Αυτό είναι ακέραιος αν και μόνο αν ο

να είναι λύση της διοφαντικής εξίσωσης

η οποία είναι η εξίσωση Pell.
Από γνωστή θεωρία, αφού η θεμελιώδης λύση είναι η

κάθε άλλη λύση είναι της μορφής

. Π.χ. για
παίρνουμε

. Για

έχουμε

που δίνει την λύση

κ.τ.λ.
Πιο συγκεκριμένα το

είναι λύση

για κάποιο φυσικό

. Η ακολουθία που δίνει τις τιμές του

είναι η

με αναδρομικό τύπο

.
Επεξεργασία: Έκανα κάποιες τροποποιήσεις αφού στην αρχική μου λύση έλυσα την

βρίσκοντας επιπλέον λύσεις. Ευχαριστώ τον Γιώργο που παρατήρησε σε π.μ. ότι είχα αυτές τις επιπλέον λύσεις.
τελευταία επεξεργασία από
Demetres σε Τετ Φεβ 06, 2013 3:11 pm, έχει επεξεργασθεί 2 φορές συνολικά.
 με
με 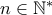 .
. .
. η διακύμανση είναι ακέραιος;
η διακύμανση είναι ακέραιος; η τυπική απόκλιση είναι ακέραιος;
η τυπική απόκλιση είναι ακέραιος;
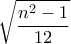 (απλό). Αυτό είναι ακέραιος αν και μόνο αν ο
(απλό). Αυτό είναι ακέραιος αν και μόνο αν ο  να είναι λύση της διοφαντικής εξίσωσης
να είναι λύση της διοφαντικής εξίσωσης  η οποία είναι η εξίσωση Pell.
η οποία είναι η εξίσωση Pell. κάθε άλλη λύση είναι της μορφής
κάθε άλλη λύση είναι της μορφής  . Π.χ. για
. Π.χ. για 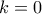 παίρνουμε
παίρνουμε  . Για
. Για  έχουμε
έχουμε  που δίνει την λύση
που δίνει την λύση  κ.τ.λ.
κ.τ.λ. για κάποιο φυσικό
για κάποιο φυσικό  . Η ακολουθία που δίνει τις τιμές του
. Η ακολουθία που δίνει τις τιμές του  με αναδρομικό τύπο
με αναδρομικό τύπο  .
. βρίσκοντας επιπλέον λύσεις. Ευχαριστώ τον Γιώργο που παρατήρησε σε π.μ. ότι είχα αυτές τις επιπλέον λύσεις.
βρίσκοντας επιπλέον λύσεις. Ευχαριστώ τον Γιώργο που παρατήρησε σε π.μ. ότι είχα αυτές τις επιπλέον λύσεις.

![\displaystyle{s^2=\frac{1}{n}\left[1^2+2^2+...+n^2-\frac{1}{n}(1+2+...+n)^2 \right]\overset{(1),(2)}=} \displaystyle{s^2=\frac{1}{n}\left[1^2+2^2+...+n^2-\frac{1}{n}(1+2+...+n)^2 \right]\overset{(1),(2)}=}](/forum/ext/geomar/texintegr/latexrender/pictures/e102809eac122ad3d73ba39b8355bf12.png)
![\displaystyle{=\frac{1}{n}\left[\frac{n(n+1)(2n+1)}{6}-\frac{1}{n}\left(\frac{n(n+1)}{2}\right)^2 \right]=...=\frac{n^2-1}{12}} \displaystyle{=\frac{1}{n}\left[\frac{n(n+1)(2n+1)}{6}-\frac{1}{n}\left(\frac{n(n+1)}{2}\right)^2 \right]=...=\frac{n^2-1}{12}}](/forum/ext/geomar/texintegr/latexrender/pictures/85ee1f264f51f97f73454fa995b74225.png) .
. δε διαιρείται με
δε διαιρείται με 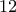 , επομένως το
, επομένως το  :
: , τότε
, τότε 
 , τότε
, τότε 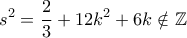
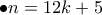 , τότε
, τότε 
 , τότε
, τότε 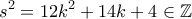
 , τότε
, τότε 
 , τότε
, τότε  .
. .
.