 ενός κύκλου
ενός κύκλου  , η οποία επιλέγεται τυχαία, είναι μεγαλύτερη από την πλευρά
, η οποία επιλέγεται τυχαία, είναι μεγαλύτερη από την πλευρά  του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου;
του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου; ενός κύκλου
ενός κύκλου  , η οποία επιλέγεται τυχαία, είναι μεγαλύτερη από την πλευρά
, η οποία επιλέγεται τυχαία, είναι μεγαλύτερη από την πλευρά  του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου;
του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου; . Προφανώς το ίδιο συμβαίνει αν φέρουμε χορδή και από τις άλλες δύο κορυφές του τριγώνου. Άρα υπάρχουν 3 ίσες περιοχές.
. Προφανώς το ίδιο συμβαίνει αν φέρουμε χορδή και από τις άλλες δύο κορυφές του τριγώνου. Άρα υπάρχουν 3 ίσες περιοχές. 

Ευχαριστώ τον Γιάννη για την άμεση και πολύ ενδιαφέρουσα προσέγγιση.giannis84 έγραψε:
 κύκλου (O, R). Φέρνουμε τις χορδές
κύκλου (O, R). Φέρνουμε τις χορδές  .
.  είναι ισόπλευρο τρίγωνο εγγεγραμμένο στον
είναι ισόπλευρο τρίγωνο εγγεγραμμένο στον 
 είναι μεταξύ των
είναι μεταξύ των  τότε το κυρτό τόξο
τότε το κυρτό τόξο  είναι μεγαλύτερο από
είναι μεγαλύτερο από  οπότε
οπότε  .
. , αφού
, αφού 
 να ταυτίζεται με τα
να ταυτίζεται με τα  ονομάζεται "υπαρκτό ενδεχόμενο μηδενικής πιθανότητας".
ονομάζεται "υπαρκτό ενδεχόμενο μηδενικής πιθανότητας". του κύκλου.
του κύκλου. . Η πιθανότητα να είναι
. Η πιθανότητα να είναι  είναι
είναι 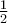 .
. μέσο χορδής
μέσο χορδής  , οπότε το
, οπότε το  είναι το απόστημα στη χορδή.
είναι το απόστημα στη χορδή. , άρα η πιθανότητα "η τυχαία χορδή
, άρα η πιθανότητα "η τυχαία χορδή  να είναι μεγαλύτερη από την πλευρά του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου"
να είναι μεγαλύτερη από την πλευρά του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου" 
 κύκλου (O, R).
κύκλου (O, R). μέσο χορδής
μέσο χορδής  , οπότε το
, οπότε το  είναι το απόστημα στη χορδή.
είναι το απόστημα στη χορδή. .
. είναι σημείο του κυκλικού δίσκου
είναι σημείο του κυκλικού δίσκου  , δηλαδή εσωτερικό του κύκλου που είναι εγγεγραμμένος στο ισόπλευρο τρίγωνο
, δηλαδή εσωτερικό του κύκλου που είναι εγγεγραμμένος στο ισόπλευρο τρίγωνο  , που είναι εγγεγραμμένο στον
, που είναι εγγεγραμμένο στον  .
. είναι
είναι  , ενώ του κυκλικού δίσκου
, ενώ του κυκλικού δίσκου  είναι
είναι  , οπότε η πιθανότητα "η τυχαία χορδή
, οπότε η πιθανότητα "η τυχαία χορδή  να είναι μεγαλύτερη από την πλευρά του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου" είναι
να είναι μεγαλύτερη από την πλευρά του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου" είναι 
![\displaystyle\Omega=[(x,y): x^2+y^2\leq1}] \displaystyle\Omega=[(x,y): x^2+y^2\leq1}]](/forum/ext/geomar/texintegr/latexrender/pictures/3a931680c3911a51e1b4a6c9b5317a3b.png)
![\displaystyle\Omega'=[(x,y):x^2+y^2\leq\frac{1}{2}] \displaystyle\Omega'=[(x,y):x^2+y^2\leq\frac{1}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/beb4ce73c5bd97b51db03a4355d950ee.png)
![\displaystyle \Omega=[(r,\theta):0\leq r \leq1, 0\leq\theta\leq\ 2\pi] \displaystyle \Omega=[(r,\theta):0\leq r \leq1, 0\leq\theta\leq\ 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/7376a1b65eef87cd70fdedbb24d1738c.png)
![\displaystyle \Omega'=[(r,\theta):0\leq r \leq \frac{1}{2}, 0\leq\theta\leq\ 2\pi] \displaystyle \Omega'=[(r,\theta):0\leq r \leq \frac{1}{2}, 0\leq\theta\leq\ 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/8cbc15c46dbd83ba4c9f8f2c571aabf6.png)

 με διάμετρο
με διάμετρο  .
. .
.  του ημικυκλίου
του ημικυκλίου ![[O, R] [O, R]](/forum/ext/geomar/texintegr/latexrender/pictures/a49915db57ec644766749b5f97e2f43b.png) .
. , δηλαδή καθώς το
, δηλαδή καθώς το  διατρέχει την ημιπεριφέρεια από το
διατρέχει την ημιπεριφέρεια από το  προς το
προς το  , το μήκος του
, το μήκος του  αυξάνει παίρνοντας τιμές στο διάστημα
αυξάνει παίρνοντας τιμές στο διάστημα ![[0, 2R] [0, 2R]](/forum/ext/geomar/texintegr/latexrender/pictures/d667002da3a1f42083939ae4b61bc73d.png) .
. είναι
είναι 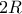 .
. ώστε "η τυχαία χορδή
ώστε "η τυχαία χορδή  να είναι μεγαλύτερη από
να είναι μεγαλύτερη από  " είναι
" είναι  .
.  , προκύπτει ότι η πιθανότητα του ενδεχομένου "η τυχαία χορδή
, προκύπτει ότι η πιθανότητα του ενδεχομένου "η τυχαία χορδή  να είναι μεγαλύτερη από την πλευρά του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου" είναι
να είναι μεγαλύτερη από την πλευρά του εγγεγραμμένου στον κύκλο ισοπλεύρου τριγώνου" είναι 
 , συμβολιζόμενη Ρ(Α), δίδεται από τη σχέση
, συμβολιζόμενη Ρ(Α), δίδεται από τη σχέση 
 είναι το εμβαδόν του ενδεχομένου Α και
είναι το εμβαδόν του ενδεχομένου Α και  είναι το εμβαδόν του δειγματικού χώρου Ω.
είναι το εμβαδόν του δειγματικού χώρου Ω. , για κάθε ενδεχόμενο Α.
, για κάθε ενδεχόμενο Α. .
. , για οποιαδήποτε δύο ενδεχόμενα Α, Β με
, για οποιαδήποτε δύο ενδεχόμενα Α, Β με  .
. ,
,
 ,
, .
. από το
από το  για να προκύψει το
για να προκύψει το  , είναι ότι το
, είναι ότι το  έχει υπολογιστεί δύο φορές, αφού το
έχει υπολογιστεί δύο φορές, αφού το  περιέχεται και στο Α και στο Β.
περιέχεται και στο Α και στο Β. αποτελείται από ένα μη κενό σύνολο
αποτελείται από ένα μη κενό σύνολο  , μια οικογένεια υποσυνόλων
, μια οικογένεια υποσυνόλων  με τις εξής ιδιότητες:
με τις εξής ιδιότητες: ,
, ,
,
![\mathbb{P}:\mathcal{F} \to [0,1] \mathbb{P}:\mathcal{F} \to [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/6e20f02b1a7511f97a51dfd891833f71.png) με τις εξής ιδιότητες
με τις εξής ιδιότητες ,
, για κάθε
για κάθε  ,
, για κάθε
για κάθε  το οποία είναι ξένα ανά δύο.
το οποία είναι ξένα ανά δύο. είναι πεπερασμένος τα πράγματα είναι απλά. Συνήθως παίρνουμε
είναι πεπερασμένος τα πράγματα είναι απλά. Συνήθως παίρνουμε  να είναι το σύνολο όλων των υποσυνόλων του
να είναι το σύνολο όλων των υποσυνόλων του  και αρκεί να μας δοθούν οι τιμές του
και αρκεί να μας δοθούν οι τιμές του  σε όλα τα μονοσύνολα για να μπορέσουμε να υπολογίσουμε τις τιμές του σε όλα τα υπόλοιπα σύνολα.
σε όλα τα μονοσύνολα για να μπορέσουμε να υπολογίσουμε τις τιμές του σε όλα τα υπόλοιπα σύνολα. όσο και στον ορισμό του
όσο και στον ορισμό του  . Στην περίπτωσή μας είναι σαφές ότι ο
. Στην περίπτωσή μας είναι σαφές ότι ο  είναι ο χώρος όλων τον χορδών του κύκλου αλλά όπως είδαμε υπάρχουν αρκετοί διαφορετικοί τρόποι να ορίσουμε την πιθανότητα
είναι ο χώρος όλων τον χορδών του κύκλου αλλά όπως είδαμε υπάρχουν αρκετοί διαφορετικοί τρόποι να ορίσουμε την πιθανότητα  σε υποσύνολα του
σε υποσύνολα του  με κάθε ένα εκ των οποίων να έχει αρκετή συμμετρία στον ορισμό του ώστε να μπορεί να θεωρηθεί ότι η τυχαία επιλογή της ευθείας γίνεται ομοιόμορφα.
με κάθε ένα εκ των οποίων να έχει αρκετή συμμετρία στον ορισμό του ώστε να μπορεί να θεωρηθεί ότι η τυχαία επιλογή της ευθείας γίνεται ομοιόμορφα. ρίχνεται τυχαία στο επίπεδο το οποίο είναι χωρισμένο με παράλληλες γραμμές σε απόσταση
ρίχνεται τυχαία στο επίπεδο το οποίο είναι χωρισμένο με παράλληλες γραμμές σε απόσταση  η μία από την άλλη. Ποια η πιθανότητα ότι η βελόνα θα διασταυρώσει μία από τις ευθείες του επιπέδου;
η μία από την άλλη. Ποια η πιθανότητα ότι η βελόνα θα διασταυρώσει μία από τις ευθείες του επιπέδου;εδώgiannis84 έγραψε:Ένα άλλο πολύ ενδιαφέρον θέμα που σχετίζεται με την έννοια της γεωμετρικής πιθανότητας είναι το πρόβλημα της βελονας του Buffon
Μία βελόνα μήκουςρίχνεται τυχαία στο επίπεδο το οποίο είναι χωρισμένο με παράλληλες γραμμές σε απόσταση
η μία από την άλλη. Ποια η πιθανότητα ότι η βελόνα θα διασταυρώσει μία από τις ευθείες του επιπέδου;
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες