
Να εξετασθεί η αλήθεια των προτάσεων:
- Το π.α.τ. έχει ακριβώς μια λύση
 η οποία ορίζεται σε ολόκληρο το διάστημα
η οποία ορίζεται σε ολόκληρο το διάστημα  .
. - Ισχύει
 .
.
edit: 27/5/23, 10:55. Διορθώθηκε τυπογραφικό.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

 η οποία ορίζεται σε ολόκληρο το διάστημα
η οποία ορίζεται σε ολόκληρο το διάστημα  .
. .
.
Αν θέσουμε

 είναι
είναι 
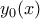 είναι γνησίως φθίνουσα οπότε το ii προκύπτει άμεσα .
είναι γνησίως φθίνουσα οπότε το ii προκύπτει άμεσα . ανοικτό διάστημα και
ανοικτό διάστημα και 
![[a,b]\subseteq I [a,b]\subseteq I](/forum/ext/geomar/texintegr/latexrender/pictures/0c821dc116e0e2afe7e0856071a2479e.png) υπάρχουν σταθερές
υπάρχουν σταθερές  ώστε
ώστε ![(x,y)\in [a,b]\times \mathbb{R} (x,y)\in [a,b]\times \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/56bf696826d3eafc07bd9ae5b488407a.png) είναι
είναι 
![x\in [a,b] x\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/a43ae7b1dc0c36150a171ced21dac8fa.png) και
και  είναι
είναι 

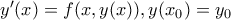

 ανοικτό διάστημα και
ανοικτό διάστημα και 
![[c,d]\subseteq I [c,d]\subseteq I](/forum/ext/geomar/texintegr/latexrender/pictures/ecef5de90c548d6662f373800415481a.png) υπάρχουν σταθερές
υπάρχουν σταθερές  ώστε
ώστε ![(x,y)\in [c,d]\times \mathbb{R} (x,y)\in [c,d]\times \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/5bf5d0c02ac86177d79e0b3d90b96677.png) είναι
είναι 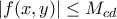
![x\in [c,d] x\in [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/8c206d8011f46956a55e3eeb997f631a.png) και
και  είναι
είναι 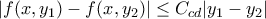

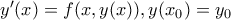

 και
και

 το μέγιστο διάστημα που ορίζεται η παραπάνω λύση.
το μέγιστο διάστημα που ορίζεται η παραπάνω λύση.
 είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του  .
.![\displaystyle [x_0-\epsilon ,b] \displaystyle [x_0-\epsilon ,b]](/forum/ext/geomar/texintegr/latexrender/pictures/7468bc0390536c3aac02f8f5a8c60b2d.png)
![\displaystyle |y'(x)|\leq M,x\in [x_0-\epsilon ,b] \displaystyle |y'(x)|\leq M,x\in [x_0-\epsilon ,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2109ed423e915e9a864c9662f621bf3b.png)


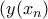 είναι βασική οπότε συγκλίνει.
είναι βασική οπότε συγκλίνει.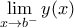 υπάρχει.
υπάρχει.
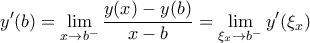


 ορίζεται στο
ορίζεται στο 
 είναι το δεξιο άκρο του
είναι το δεξιο άκρο του 
 είναι το αριστερό άκρο του
είναι το αριστερό άκρο του  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 22 επισκέπτες