Ορισμένο ολοκλήρωμα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Ορισμένο ολοκλήρωμα
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 12:51 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Ορισμένο ολοκλήρωμα
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 12:51 pm, έχει επεξεργασθεί 2 φορές συνολικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ορισμένο ολοκλήρωμα
Επειδή έγινε συζήτηση στα προηγούμενα ποστ, είναι προφανές από την εκφώνηση ότι τα μεταβλητά μεγέθη είναι ταorestisgotsis έγραψε: ↑Τετ Απρ 05, 2023 8:01 pmΤαικανοποιούν την
για
(
).
Βρείτε τις τιμές τωνγια τις οποίες ελαχιστοποιείται το παρακάτω ορισμένο
ολοκλήρωμα και στη συνέχεια την ελάχιστη τιμή του:.
 . Άλλωστε δεν έχει νόημα να ψάχνουμε το ελάχιστο του ολοκληρώματος θεωρώντας μεταβλητά τα
. Άλλωστε δεν έχει νόημα να ψάχνουμε το ελάχιστο του ολοκληρώματος θεωρώντας μεταβλητά τα  για τον απλούστατο λόγο ότι παίρνοντας
για τον απλούστατο λόγο ότι παίρνοντας  το (θετικό) ολοκλήρωμα τείνει στο
το (θετικό) ολοκλήρωμα τείνει στο  . Μάλιστα δεν λαμβάνει ποτέ την τιμή
. Μάλιστα δεν λαμβάνει ποτέ την τιμή  για προφανείς λόγους.
για προφανείς λόγους. Πίσω στην άσκηση.
Θα δούμε ότι η ελάχιστη τιμή το ολοκληρώματος λαμβάνεται από την
 . Πράγματι, από την
. Πράγματι, από την  έχουμε ότι ικανοποιείται η ανισότητα
έχουμε ότι ικανοποιείται η ανισότητα  διότι
διότι .
. 'Εστω τώρα
 οποιαδήποτε με
οποιαδήποτε με  . Ειδικά για
. Ειδικά για  έπεται
έπεται  .
. Θα δείξουμε ότι η τιμή του δοθέντος ολοκληρώματος είναι μεγαλύτερη από την αντίστοιχη με
 στην θέση των
στην θέση των  . Πράγματι,
. Πράγματι, 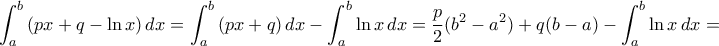

![\displaystyle{ =\left [ \left ( \dfrac {b^2-a^2}{a+b} -(b-a) \right ) + \left ( \ln \dfrac {a+b}{2}\right ) (b-a) \right ] - \int_{a}^{b}\ln x\,dx = \int _a^b \left ( \dfrac {2x}{a+b} -1 +\ln \dfrac {a+b}{2} \right ) dx - \int_{a}^{b}\ln x\,dx = } \displaystyle{ =\left [ \left ( \dfrac {b^2-a^2}{a+b} -(b-a) \right ) + \left ( \ln \dfrac {a+b}{2}\right ) (b-a) \right ] - \int_{a}^{b}\ln x\,dx = \int _a^b \left ( \dfrac {2x}{a+b} -1 +\ln \dfrac {a+b}{2} \right ) dx - \int_{a}^{b}\ln x\,dx = }](/forum/ext/geomar/texintegr/latexrender/pictures/ad3da754a074301f7dc0db0195ed1b53.png)
 , όπως θέλαμε.
, όπως θέλαμε.Αν θέλουμε και την τιμή του ελάχιστου ολοκληρώματος, είναι άμεση από το προηγούμενο και το
 .
.
τελευταία επεξεργασία από Mihalis_Lambrou σε Σάβ Απρ 08, 2023 11:45 am, έχει επεξεργασθεί 1 φορά συνολικά.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
