Ένα όριο

Tolaso J Kos · #1

Έστω $f:[0, 1] \rightarrow (0, +\infty)$ συνεχής συνάρτηση και $\mathcal{A}$ το σύνολο όλων των θετικών ακεραίων

για τους οποίους υπάρχει x_n

ώστε $\displaystyle{\int_{x_n}^{1} f(t) \, \mathrm{d}t = \frac{1}{n}}$ . Να δειχθεί ότι η $\{x_n\}_{n \in \mathcal{A}}$ είναι άπειρη και να υπολογιστεί το όριο

$\displaystyle \ell = \lim_{n \rightarrow +\infty} n \left( x_n -1 \right)$

ΑλέξανδροςΚ · #2

Αφού $f \in \mathcal{C}([0,1], (0,+\infty))$ έχουμε ότι $a = \int_{0}^{1}f(x)dx > 0$ .
Θεωρούμε την απεικόνιση $g: [0,1] \to (0,+\infty), \hspace{2mm} t \mapsto \int_{t}^{1}f(x)dx$ . Προφανώς, η

είναι συνεχώς παραγωγίσιμη, γνησίως φθίνουσα και το σύνολο τιμών της είναι το κλειστό διάστημα [0,a]

.
Από την Αρχιμήδεια ιδιότητα των πραγματικών αριθμών έχουμε ότι υπάρχει $n_{0} \in \mathbb{N}$ τέτοιο ώστε για κάθε $n \geq n_{0}$ ισχύει $\frac{1}{n} < a$ . Επομένως, από το Θεώρημα Ενδιάμεσης Τιμής έχουμε ότι για κάθε $n \geq n_{0}$ υπάρχει $x_{n} \in (0,1)$ ώστε $g(x_{n}) = \frac{1}{n}$ . Εκμεταλλευόμενοι της γνήσιας μονοτονίας της

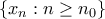μπορούμε μάλιστα να συμπεράνουμε ότι η ακολουθία $\{x_{n}: n \geq n_{0}\}$ είναι γνησίως αύξουσα. Προφανώς 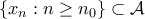$\{x_{n}: n \geq n_{0}\} \subset \mathcal{A}$ και ως εκ τούτου το σύνολο $\mathcal{A}$ είναι άπειρο.

Σταθεροποιούμε $n \geq n_{0}$ τυχόν. Εφαρμόζουμε το Θεώρημα Μέσης Τιμής στην απεικόνιση

στο διάστημα $[x_{n},1]$ .
Τότε, υπάρχει $\xi_{n} \in [x_{n},1]$ τέτοιο ώστε $g^{\prime}(\xi_{n}) = -f(\xi_{n}) = \frac{g(1) - g(x_{n})}{1-x_{n}}$ . Επομένως
$n(1-x_{n}) = \frac{1}{f(\xi_{n})}$ . Θα αποδείξουμε ότι $\lim_{n \to \infty}x_{n} = 1$ . Τότε από το κριτήριο παρεμβολής έχουμε ότι και $\lim_{n \to \infty} \xi_{n} = 1$ και άρα λόγω της συνέχειας της

έχουμε ότι $\lim_{n \to \infty}n(x_{n}-1) = -\frac{1}{f(1)}$ . Καταφέραμε λοιπόν να υπολογίσουμε το ζητούμενο όριο.

Ξέρουμε ότι η ακολουθία $(x_{n})_{n \geq n_{0}}$ είναι γνησίως αύξουσα και άνω φραγμένη από το 1. Επομένως υπάρχει το όριο $l = lim_{n \to \infty}x_{n}$ . Έχουμε τότε ότι $g(l) = lim_{n \to \infty}g(x_{n}) = lim_{n \to \infty }\frac{1}{n} = 0$ και άρα αναγκαστικά έχουμε ότι l = 1

.

Ένα όριο

Ένα όριο

Re: Ένα όριο

Μέλη σε σύνδεση