Έστω
 μια συνεχής και άνω φραγμένη συνάρτηση, και έστω
μια συνεχής και άνω φραγμένη συνάρτηση, και έστω  . Να αποδείξετε ότι για κάθε
. Να αποδείξετε ότι για κάθε  υπάρχει ρητός
υπάρχει ρητός  τέτοιος ώστε
τέτοιος ώστε  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 μια συνεχής και άνω φραγμένη συνάρτηση, και έστω
μια συνεχής και άνω φραγμένη συνάρτηση, και έστω  . Να αποδείξετε ότι για κάθε
. Να αποδείξετε ότι για κάθε  υπάρχει ρητός
υπάρχει ρητός  τέτοιος ώστε
τέτοιος ώστε  .
.H ουσία είναι η πυκνότητα των ρητών.Ορέστης Λιγνός έγραψε: ↑Σάβ Ιαν 28, 2023 1:53 pmΤο παρακάτω πρόβλημα αποτέλεσε θέμα της χθεσινής εξέτασης του μαθήματος πρώτου εξαμήνου "Ανάλυση Ι & Εφαρμογές" του Φυσικού τμήματος του ΕΚΠΑ. Έχω βρει μια λύση αλλά πιστεύω υπάρχει κάτι απλούστερο που μου διαφεύγει.
Έστωμια συνεχής και άνω φραγμένη συνάρτηση, και έστω
. Να αποδείξετε ότι για κάθε
υπάρχει ρητός
τέτοιος ώστε
.
 τέτοιο ώστε
τέτοιο ώστε  . Από την συνέχεια της
. Από την συνέχεια της  στο
στο  υπάρχει
υπάρχει  τέτοιο ώστε για
τέτοιο ώστε για  με
με  ισχύει
ισχύει  . Ειδικά, για ένα οποιοδήποτε τέτοιο
. Ειδικά, για ένα οποιοδήποτε τέτοιο  ισχύει
ισχύει  .
.  στην
στην  να το επιλέξουμε ρητό, και τελειώσαμε.
να το επιλέξουμε ρητό, και τελειώσαμε.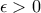 . Υποθέτουμε πως
. Υποθέτουμε πως  για κάθε ρητό
για κάθε ρητό  . Αφού
. Αφού  , υπάρχει
, υπάρχει  τέτοιο ώστε
τέτοιο ώστε  . Θεωρούμε ακολουθία
. Θεωρούμε ακολουθία  ρητών αριθμών τέτοια ώστε
ρητών αριθμών τέτοια ώστε  (τέτοια ακολουθία υπάρχει λόγω της πυκνότητας των ρητών). Τότε, από την Αρχή της Μεταφοράς,
(τέτοια ακολουθία υπάρχει λόγω της πυκνότητας των ρητών). Τότε, από την Αρχή της Μεταφοράς, , και αφού
, και αφού  , προκύπτει ότι
, προκύπτει ότι
 το supremum, υπάρχει ακολουθία
το supremum, υπάρχει ακολουθία  με
με  .
.  σταθερό. Από την πυκνότητα των ρητών και την συνέχεια της
σταθερό. Από την πυκνότητα των ρητών και την συνέχεια της  στο
στο  , υπάρχει ρητός, ας τον πούμε
, υπάρχει ρητός, ας τον πούμε  , με
, με  .To κάνουμε αυτό για όλα τα
.To κάνουμε αυτό για όλα τα  . Είναι τότε
. Είναι τότε  .
. . Οπότε αργά ή γρήγορα ισχύει η ζητούμενη
. Οπότε αργά ή γρήγορα ισχύει η ζητούμενη  .
. είναι supremum παίζει δευτερεύοντα ρόλο. Αυτό που χρειάζεται είναι ότι υπάρχει ακολουθία
είναι supremum παίζει δευτερεύοντα ρόλο. Αυτό που χρειάζεται είναι ότι υπάρχει ακολουθία  με
με  . Έπεται ότι θα υπάρχει τότε ακολουθία ρητών
. Έπεται ότι θα υπάρχει τότε ακολουθία ρητών  με
με  .
.Mihalis_Lambrou έγραψε: ↑Δευ Ιαν 30, 2023 11:30 pmΛίγο αλλιώς: Αφούτο supremum, υπάρχει ακολουθία
με
.
Κρατάμε τώρα τοσταθερό. Από την πυκνότητα των ρητών και την συνέχεια της
στο
, υπάρχει ρητός, ας τον πούμε
, με
.To κάνουμε αυτό για όλα τα
. Είναι τότε
.
Δηλαδή. Οπότε αργά ή γρήγορα ισχύει η ζητούμενη
.
Σxολιάζω ότι το γεγονός ότι τοείναι supremum παίζει δευτερεύοντα ρόλο. Αυτό που χρειάζεται είναι ότι υπάρχει ακολουθία
με
. Έπεται ότι θα υπάρχει τότε ακολουθία ρητών
με
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες