Σειρά με αριθμούς Fibonacci

ksofsa · #1

Καλημέρα!

Στο λήμμα της Wikipedia για την ακολουθία Fibonacci καταγράφεται η παρακάτω ισότητα:

$\sum_{k=0}^{\infty }\dfrac{1}{F_{2k+1}+1}=\dfrac{\sqrt{5}}{2}$ .

Μπορείτε να υπολογίσετε τη δίδυμη σειρά:

$\sum_{k=1}^{\infty }\dfrac{1}{F_{2k+1}-1}$ ;

Tolaso J Kos · #2

ksofsa έγραψε: ↑
Παρ Ιαν 27, 2023 8:12 am
Μπορείτε να υπολογίσετε τη δίδυμη σειρά:

$\sum_{k=1}^{\infty }\dfrac{1}{F_{2k+1}-1}$ ;

Δε πιστεύω ότι έχει κλειστό τύπο η συγκεκριμένη σειρά.

Η πρώτη σειρά , ας πούμε , χρησιμοποιώντας το τύπο του Binet βγαίνει εύκολα:

$\displaystyle{\begin{aligned} \sum_{n=0}^N\frac{1}{1+F_{2n+1}}&= \sum_{n=0}^N\frac{1}{1+\frac{\varphi^{2n+1}+\varphi^{-(2n+1)}}{\sqrt{5}}} \\ &= \sqrt{5} \sum_{n=0}^{N}\frac{\varphi^{2n+1}}{\varphi^{2(2n+1)}+\sqrt{5}\varphi^{2n+1}+1} \\ &=\sqrt{5} \sum_{n=0}^{N}\frac{\varphi^{2n+1}}{(\varphi^{2n+1}+\varphi)\left( \varphi^{2n+1}+\frac{1}{\varphi}\right)}\\ &= \sqrt{5} \sum_{n=0}^{N}\frac{\varphi^{2n+1}}{(\varphi^{2n}+1)\left( \varphi^{2n+2}+1\right)} \\ &= \frac{\varphi\sqrt{5}}{1-\varphi^2}\sum_{n=0}^N\left(\frac{\varphi^{2n}}{1+\varphi^{2n}}-\frac{\varphi^{2n+2}}{1+\varphi^{2n+2}} \right) \\ &=\sqrt{5}\left(\frac{\varphi^{2N+2}}{1+\varphi^{2N+2}} -\frac{1}{2}\right) \end{aligned}}$

Κάνοντας το ίδιο για τη δεύτερη δε βλέπω κάτι ωραίο. Μπορεί να κάνω και λάθος ... δε θα είναι η πρώτη φορά εξάλλου. Γενικά οι σειρές τέτοιου τύπου αν δεν είναι "στημένες" δύσκολα πέφτουν. π.χ $\displaystyle{\sum_{n=0}^{\infty} \frac{1}{F_{2n+1}} = \frac{\sqrt{5}}{4} \vartheta_2^2 \left ( \frac{3- \sqrt{5}}{2} \right )}$ .

ksofsa · #3

Καλησπέρα Τόλη!

Δίνω ισχυρή υπόδειξη:

Δοκιμάστε να υπολογίσετε πρώτα τη σειρά:

$\sum_{n=1}^{\infty }\dfrac{F_{2n+1}}{F_{2n+1}^2-1}$ .

Tolaso J Kos · #4

Καταλαβαίνω γιατί μου το δίνεις ... Δίνω την αρχική μου προσπάθεια;

$\displaystyle{\begin{aligned} \sum_{n=1}^{N} \frac{1}{\mathcal{F}_{2n+1} - 1} &= \sum_{n=1}^{N} \frac{1}{\frac{\varphi^{2n+1} + \varphi^{-(2n+1)}}{\sqrt{5}} -1} \\ &=\sqrt{5} \sum_{n=1}^{\infty} \frac{\varphi^{2n+1}}{\varphi^{2(2n+1)} - \sqrt{5} \varphi^{2n+1} + 1} \\ &=\sqrt{5} \sum_{n=1}^{N} \frac{\varphi^{2n+1}}{\left ( \varphi^{2n+1} - \varphi \right ) \left ( \varphi^{2n+1} - \frac{1}{\varphi} \right )} \\ &=\sqrt{5} \sum_{n=1}^{N} \frac{\varphi^{2n+1}}{\left ( \varphi^{2n} - 1 \right ) \left ( \varphi^{2n+2} - \varphi \right )} \\ &= \sqrt{5} \sum_{n=1}^{N} \frac{\varphi^{2n}}{\left ( \varphi^{2n} - 1 \right ) \left ( \varphi^{2n+1} - 1 \right )} \end{aligned}}$
Νομίζω κάτι παραβλέπω στο τελευταίο βήμα... Αν το τηλεσκοπήσουμε τότε τελειώσαμε.

ksofsa · #5

Η λύση όντως ανάγεται σε τηλεσκοπικό άθροισμα:

$\sum_{n=1}^{\infty }\dfrac{F_{2n+1}}{F_{2n+1}^2-1}=\sum_{n=1}^{\infty }\dfrac{F_{2n+2}-F_{2n}}{F_{2n}F_{2n+2}}=\sum_{n=1}^{\infty }(\dfrac{1}{F_{2n}}-\dfrac{1}{F_{2n+2}})=\dfrac{1}{F_{2}}=1$

Συνεπώς,

$\sum_{n=1}^{\infty }(\dfrac{1}{F_{2n+1}-1}+\dfrac{1}{F_{2n+1}+1})=2\sum_{n=1}^{\infty }\dfrac{F_{2n+1}}{F_{2n+1}^2-1}=2$

και άρα

$\sum_{n=1}^{\infty }\dfrac{1}{F_{2n+1}-1}=2-\dfrac{\sqrt{5}-1}{2}=\dfrac{5-\sqrt{5}}{2}$ .

Τόλη, επειδή η ιδέα στον πυρήνα της λύσης είναι το τηλεσκοπικό άθροισμα, πιθανολογώ ότι το άθροισμα στη λύση σου θα μπορούσε όντως να αναχθεί σε τηλεσκοπικό.Έγραψα την πιο πάνω λύση, ώστε ενδεχομένως να βοηθήσει στη μετατροπή σε τηλεσκοπική σειρά.

Tolaso J Kos · #6

ksofsa έγραψε: ↑
Πέμ Φεβ 02, 2023 10:30 pm

... πιθανολογώ ότι το άθροισμα στη λύση σου θα μπορούσε όντως να αναχθεί σε τηλεσκοπικό. ...

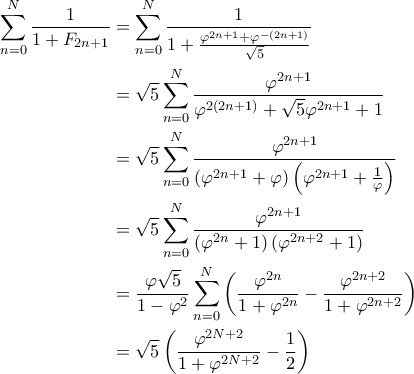
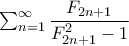Το πιο πιθανό είναι κάπως να τηλεσκοπεί, αλλά δε το βλέπω. Το άθροισμα που έγραψες είναι εύκολο χρησιμοποιώντας το γεγονός ότι $\displaystyle{\mathcal{F}^2_{2n+1} - 1 = \mathcal{F}_{2n} \mathcal{F}_{2n+2}}$ (ταυτότητα Cassini) και το γεγονός ότι $\displaystyle{\mathcal{F}_{2n+2} - \mathcal{F}_{2n} = \mathcal{F}_{2n+1}}$ . Μετά είναι εύκολο!

Anyway ... !!

Σειρά με αριθμούς Fibonacci

Σειρά με αριθμούς Fibonacci

Re: Σειρά με αριθμούς Fibonacci

Re: Σειρά με αριθμούς Fibonacci

Re: Σειρά με αριθμούς Fibonacci

Re: Σειρά με αριθμούς Fibonacci

Re: Σειρά με αριθμούς Fibonacci

Μέλη σε σύνδεση