TrItOs έγραψε: ↑Σάβ Ιουν 25, 2022 8:52 pm
Πρόβλημα(2): Έστω

ένας χωρος

και έστω

ένας αυτοσυζυγης τελεστής για τον οποίο ισχύει
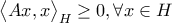
. Να δειχθεί ότι

....
Για το πρόβλημα(2) γνωρίζουμε ότι:

,

για οποιοδήποτε
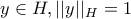
, έχει πραγματικές ιδιοτιμές.
Ίσως υπάρχει τρόπος απόδειξης σύμφωνα με την υπόδειξη που δείνεις (δεν το κοίταξα αλλά βλέπε παρακάτω) όμως δίνω έναν διαφορετικό. Θα χρειαστώ α) κάθε συνεχής τελεστής ικανοποιεί
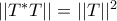
και β) κάθε θετικός τελεστής

έχει τετραγωνική ρίζα, δηλαδή υπάρχει

θετικός (και άρα αυτοσυζυγής) με

. Και τα δύο αυτά υπάρχουν σε όλα τα βιβλία Θεωρίας Τελεστών σε χώρους Hilbert.
Άρα


, όπως θέλαμε.
Σχολιάζω ότι υπάρχει και μία γενικότερη ανισότητα τύπου Cauchy-Schwarz, συγκεκριμένα η
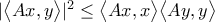
, από την οποία σίγουρα βγαίνει η αποδεικτέα. Δεν το κοίταξα (ακόμα δεν ... ξύπνησα) αλλά μάλλον για την απόδειξή της χρειάζεται τα ίδια υλικά με την απόδειξη που μόλις έγραψα, οπότε έβαλα την παραπάνω για λόγους πληρότητας.
![k \in C \big( [0,1] \times [0,1] : \mathbb{C} \big) k \in C \big( [0,1] \times [0,1] : \mathbb{C} \big)](/forum/ext/geomar/texintegr/latexrender/pictures/3aedf4809097e97b587c1ca14421de6a.png) και έστω ο τελεστής
και έστω ο τελεστής  με τύπο
με τύπο![\displaystyle{ (Au)(x) = \int\limits_{0}^{x} k(x,y) u(y) d y , x \in [0,1] } \displaystyle{ (Au)(x) = \int\limits_{0}^{x} k(x,y) u(y) d y , x \in [0,1] }](/forum/ext/geomar/texintegr/latexrender/pictures/46664b97b3a4e4f89a915c9f8296016c.png) .
.![X = \Big( C \big( [0,1] : \mathbb{C} \big) , || \cdot ||_{\infty} = \sup \big \{ | \cdot | : 0 \leq \cdot \leq 1 \big \} \Big) X = \Big( C \big( [0,1] : \mathbb{C} \big) , || \cdot ||_{\infty} = \sup \big \{ | \cdot | : 0 \leq \cdot \leq 1 \big \} \Big)](/forum/ext/geomar/texintegr/latexrender/pictures/9eaf4723c9e070750f3520c8a8ef8cf7.png) .
.

 ένας χωρος
ένας χωρος  και έστω
και έστω  ένας αυτοσυζυγης τελεστής για τον οποίο ισχύει
ένας αυτοσυζυγης τελεστής για τον οποίο ισχύει 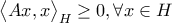 . Να δειχθεί ότι
. Να δειχθεί ότι 
 , το
, το  είναι συμπαγές και
είναι συμπαγές και 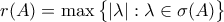 .
. ,
,  για οποιοδήποτε
για οποιοδήποτε 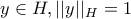 , έχει πραγματικές ιδιοτιμές.
, έχει πραγματικές ιδιοτιμές.
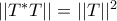 και β) κάθε θετικός τελεστής
και β) κάθε θετικός τελεστής  έχει τετραγωνική ρίζα, δηλαδή υπάρχει
έχει τετραγωνική ρίζα, δηλαδή υπάρχει  θετικός (και άρα αυτοσυζυγής) με
θετικός (και άρα αυτοσυζυγής) με  . Και τα δύο αυτά υπάρχουν σε όλα τα βιβλία Θεωρίας Τελεστών σε χώρους Hilbert.
. Και τα δύο αυτά υπάρχουν σε όλα τα βιβλία Θεωρίας Τελεστών σε χώρους Hilbert. 
 , όπως θέλαμε.
, όπως θέλαμε. 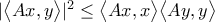 , από την οποία σίγουρα βγαίνει η αποδεικτέα. Δεν το κοίταξα (ακόμα δεν ... ξύπνησα) αλλά μάλλον για την απόδειξή της χρειάζεται τα ίδια υλικά με την απόδειξη που μόλις έγραψα, οπότε έβαλα την παραπάνω για λόγους πληρότητας.
, από την οποία σίγουρα βγαίνει η αποδεικτέα. Δεν το κοίταξα (ακόμα δεν ... ξύπνησα) αλλά μάλλον για την απόδειξή της χρειάζεται τα ίδια υλικά με την απόδειξη που μόλις έγραψα, οπότε έβαλα την παραπάνω για λόγους πληρότητας. (η απάντηση εξαρτάται από τον εκάστοτε συγκεκριμένο
(η απάντηση εξαρτάται από τον εκάστοτε συγκεκριμένο  ανήκει στο φάσμα τους (διότι είναι μη αντιστρέψιμοι) και β) τα μη-μηδενικά στοιχεία του φάσματος είναι οι ιδιοτιμές τους. Με άλλα λόγια ισχύει
ανήκει στο φάσμα τους (διότι είναι μη αντιστρέψιμοι) και β) τα μη-μηδενικά στοιχεία του φάσματος είναι οι ιδιοτιμές τους. Με άλλα λόγια ισχύει  .
.