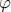 η συνάρτηση φι του Euler. Να δειχθεί ότι:
η συνάρτηση φι του Euler. Να δειχθεί ότι:
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
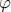 η συνάρτηση φι του Euler. Να δειχθεί ότι:
η συνάρτηση φι του Euler. Να δειχθεί ότι:

 Προφανώς
Προφανώς  . Επίσης
. Επίσης
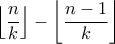 ισούται με
ισούται με  αν
αν 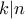 και
και  αν
αν  .
. αφού τότε το ζητούμενο προκύπτει εύκολα επαγωγικά.
αφού τότε το ζητούμενο προκύπτει εύκολα επαγωγικά. τότε προφανώς
τότε προφανώς  για κάποιο
για κάποιο  . Για
. Για  έστω
έστω  το σύνολο όλων των
το σύνολο όλων των  ώστε
ώστε  . Κάθε στοιχείο του
. Κάθε στοιχείο του  είναι της μορφής
είναι της μορφής  με
με  . Επομένως
. Επομένως  .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες