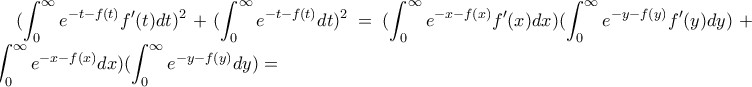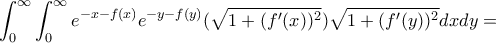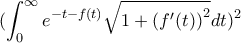θετική, αύξουσα και παραγωγίσιμη συνάρτηση. Να αποδειχτεί ότι:
θετική, αύξουσα και παραγωγίσιμη συνάρτηση. Να αποδειχτεί ότι: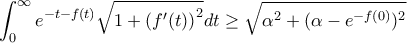
όπου

Η άσκηση δεν γνωρίζω από που προέρχεται, την είχα δει πριν καιρό σε κάποιο pdf σημειώσεων για ανισώσεις το οποίο δεν μπορώ να βρω.
Δεν έχω λύση ακόμη, αλλά θυμίζει αρκετά επικαμπύλιο και το δουλεύω σε αυτήν την κατεύθυνση.
Edit: Μετά από διάφορες προσπάθειες η μόνη που απέδωσε κάτι ήταν η εξής:
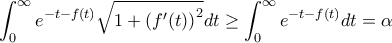

Υψώνουμε στο τετράγωνο, προσθέτουμε και παίρνουμε τη ρίζα οπότε έχουμε
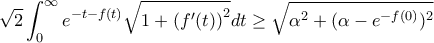
όμως η εκτίμηση δεν είναι αρκετά καλή.

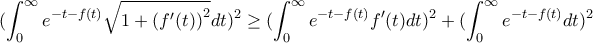

 ).
).