 ,
,  ,
,  αντίστοιχα. Να βρεθεί το μέγιστο εμβαδόν τριγώνου του οποίου η κάθε κορυφή βρίσκεται και σε διαφορετικό κύκλο όπως φαίνεται στο σχήμα.
αντίστοιχα. Να βρεθεί το μέγιστο εμβαδόν τριγώνου του οποίου η κάθε κορυφή βρίσκεται και σε διαφορετικό κύκλο όπως φαίνεται στο σχήμα.![\displaystyle{\begin{tikzpicture}
\foreach \i in {1, 2, 3}
{
\draw (0, 0) circle(\i cm);
}
\draw[dashed, red!60!black, line width=1.6pt] (1, 0) -- (-2.27, 1.96) -- (-1.01, -1.73) -- cycle;
\draw (1, 0) node[above right]{A};
\draw (-2.27, 1.96) node[left]{C};
\draw (-1.01, -1.73) node[below]{B};
\draw[fill=black] (0, 0) circle(2pt);
\end{tikzpicture}} \displaystyle{\begin{tikzpicture}
\foreach \i in {1, 2, 3}
{
\draw (0, 0) circle(\i cm);
}
\draw[dashed, red!60!black, line width=1.6pt] (1, 0) -- (-2.27, 1.96) -- (-1.01, -1.73) -- cycle;
\draw (1, 0) node[above right]{A};
\draw (-2.27, 1.96) node[left]{C};
\draw (-1.01, -1.73) node[below]{B};
\draw[fill=black] (0, 0) circle(2pt);
\end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/1077b2d6ccc030dfc63e35f7a8a97af1.png)
Άνευ λύσης.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 ,
,  ,
,  αντίστοιχα. Να βρεθεί το μέγιστο εμβαδόν τριγώνου του οποίου η κάθε κορυφή βρίσκεται και σε διαφορετικό κύκλο όπως φαίνεται στο σχήμα.
αντίστοιχα. Να βρεθεί το μέγιστο εμβαδόν τριγώνου του οποίου η κάθε κορυφή βρίσκεται και σε διαφορετικό κύκλο όπως φαίνεται στο σχήμα.![\displaystyle{\begin{tikzpicture}
\foreach \i in {1, 2, 3}
{
\draw (0, 0) circle(\i cm);
}
\draw[dashed, red!60!black, line width=1.6pt] (1, 0) -- (-2.27, 1.96) -- (-1.01, -1.73) -- cycle;
\draw (1, 0) node[above right]{A};
\draw (-2.27, 1.96) node[left]{C};
\draw (-1.01, -1.73) node[below]{B};
\draw[fill=black] (0, 0) circle(2pt);
\end{tikzpicture}} \displaystyle{\begin{tikzpicture}
\foreach \i in {1, 2, 3}
{
\draw (0, 0) circle(\i cm);
}
\draw[dashed, red!60!black, line width=1.6pt] (1, 0) -- (-2.27, 1.96) -- (-1.01, -1.73) -- cycle;
\draw (1, 0) node[above right]{A};
\draw (-2.27, 1.96) node[left]{C};
\draw (-1.01, -1.73) node[below]{B};
\draw[fill=black] (0, 0) circle(2pt);
\end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/1077b2d6ccc030dfc63e35f7a8a97af1.png)

Χωρίς τις πράξεις από την παραγώγιση και πέρα, γιατί δεν τολμώ να τις κάνω.Tolaso J Kos έγραψε: ↑Πέμ Ιούλ 08, 2021 8:00 pmΈστω ομόκεντροι κύκλοι με κέντρο την αρχή των αξόνων και ακτίνες,
,
αντίστοιχα. Να βρεθεί το μέγιστο εμβαδόν τριγώνου του οποίου η κάθε κορυφή βρίσκεται και σε διαφορετικό κύκλο όπως φαίνεται στο σχήμα.
 είναι παράλληλη του άξονα των
είναι παράλληλη του άξονα των  .
.  , είναι σαφές ότι η κορυφή
, είναι σαφές ότι η κορυφή  του τριγώνου είναι στον βόρειο αυτό πόλο (σε οποιαδήποτε άλλη θέση, το ύψος του τριγώνου θα ήταν μικρότερο και άρα δεν θα είχαμε το μέγιστο εμβαδόν).
του τριγώνου είναι στον βόρειο αυτό πόλο (σε οποιαδήποτε άλλη θέση, το ύψος του τριγώνου θα ήταν μικρότερο και άρα δεν θα είχαμε το μέγιστο εμβαδόν).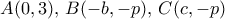 για κάποια θετικά
για κάποια θετικά 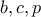 . Tα
. Tα 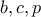 ικανοποιούν
ικανοποιούν 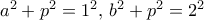 . To εμβαδόν του τριγώνου είναι
. To εμβαδόν του τριγώνου είναι 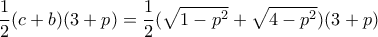 .
.  . Δεν το έκανα γιατί οδηγεί σε επίπονες πράξεις. Άλλωστε δεν πιστεύω ότι η παράσταση που θα βγει, μπορεί να επιλυθεί.
. Δεν το έκανα γιατί οδηγεί σε επίπονες πράξεις. Άλλωστε δεν πιστεύω ότι η παράσταση που θα βγει, μπορεί να επιλυθεί. θα είναι το ορθόκεντρο του
θα είναι το ορθόκεντρο του  και επειδή
και επειδή 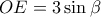 θα είναι
θα είναι
 και λύνοντας την εξίσωση βρίσκω τρείς ρίζες
και λύνοντας την εξίσωση βρίσκω τρείς ρίζες
 είναι
είναι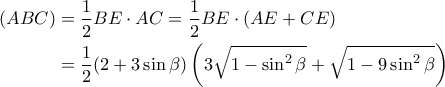
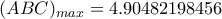
Στα χνάρια του Μιχάλη.Tolaso J Kos έγραψε: ↑Πέμ Ιούλ 08, 2021 8:00 pmΈστω ομόκεντροι κύκλοι με κέντρο την αρχή των αξόνων και ακτίνες,
,
αντίστοιχα. Να βρεθεί το μέγιστο εμβαδόν τριγώνου του οποίου η κάθε κορυφή βρίσκεται και σε διαφορετικό κύκλο όπως φαίνεται στο σχήμα.
Άνευ λύσης.
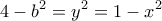 με
με 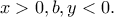

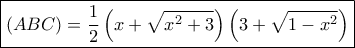
 μέγιστο εμβαδόν
μέγιστο εμβαδόν 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 23 επισκέπτες