![f:[0,1] \to [0,1] f:[0,1] \to [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/daf29ff804c14856d33ff5454116a177.png) είναι συνεχής, 1-1 και επί. Να βρεθεί το σύνολο
είναι συνεχής, 1-1 και επί. Να βρεθεί το σύνολο![\mathcal{A}= \{|f(x)-f(y)|/ x,y \in [0,1]- \mathbb{Q} \} \mathcal{A}= \{|f(x)-f(y)|/ x,y \in [0,1]- \mathbb{Q} \}](/forum/ext/geomar/texintegr/latexrender/pictures/67027b200b693e70f098932fdf3f2988.png)
Φιλικά
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![f:[0,1] \to [0,1] f:[0,1] \to [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/daf29ff804c14856d33ff5454116a177.png) είναι συνεχής, 1-1 και επί. Να βρεθεί το σύνολο
είναι συνεχής, 1-1 και επί. Να βρεθεί το σύνολο![\mathcal{A}= \{|f(x)-f(y)|/ x,y \in [0,1]- \mathbb{Q} \} \mathcal{A}= \{|f(x)-f(y)|/ x,y \in [0,1]- \mathbb{Q} \}](/forum/ext/geomar/texintegr/latexrender/pictures/67027b200b693e70f098932fdf3f2988.png)
 ειναι γνησιως μονοτονη και ετσι, αφου ειναι επι,
ειναι γνησιως μονοτονη και ετσι, αφου ειναι επι,  . Υποθετουμε οτι ειναι αυξουσα (αλλιως θεωρουμε την
. Υποθετουμε οτι ειναι αυξουσα (αλλιως θεωρουμε την 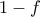 ) οποτε
) οποτε  .
.![A \subseteq [0,1] A \subseteq [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/b3a1a5540698673106ebfb68894eeaaf.png) και
και  (οι μονοι
(οι μονοι  με
με  ειναι ρητοι).
ειναι ρητοι). . Τοτε, το συνολο
. Τοτε, το συνολο ![S \subseteq [0,1] \times [0,1] S \subseteq [0,1] \times [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/46ab096d73971ed8d424dcd4b42e2def.png) των ζευγων
των ζευγων  με
με 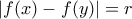 ειναι υπεραριθμησιμο (για καθε
ειναι υπεραριθμησιμο (για καθε ![x \in \left[ 0, f^{-1} (1-r) \right] x \in \left[ 0, f^{-1} (1-r) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a5018ef904afb4f2888f3a7f3d3d8a96.png) υπαρχει το καταλληλο
υπαρχει το καταλληλο  ). Αυτο το καταλληλο
). Αυτο το καταλληλο  ειναι μοναδικο (λογω μονοτονιας) οποτε τα
ειναι μοναδικο (λογω μονοτονιας) οποτε τα ![S \cap \left( \mathbb{Q} \times [0,1] \right) S \cap \left( \mathbb{Q} \times [0,1] \right)](/forum/ext/geomar/texintegr/latexrender/pictures/04123575a97b5e5db1ad374d6c2c61f4.png) και
και ![S \cap \left( [0,1] \times \mathbb{Q} \right) S \cap \left( [0,1] \times \mathbb{Q} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/a7022c9f3eacb8e414e235581476d994.png) ειναι αριθμησιμα. Κατα συνεπεια, υπαρχει ζευγος αρρητων
ειναι αριθμησιμα. Κατα συνεπεια, υπαρχει ζευγος αρρητων  με
με 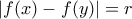 .
.  .
.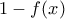 . Τότε
. Τότε  και
και  , άρα
, άρα  . Εξ' άλλου είναι προφανές ότι
. Εξ' άλλου είναι προφανές ότι  άρα
άρα  . Έστω
. Έστω  . Τότε υπάρχει
. Τότε υπάρχει  με
με  . Ονομάζω
. Ονομάζω  το σύνολο των αρρήτων του διαστήματος
το σύνολο των αρρήτων του διαστήματος 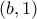 . Έστω
. Έστω  , τότε υπάρχει μοναδικό
, τότε υπάρχει μοναδικό  ώστε
ώστε  . Έστω ότι για κάθε
. Έστω ότι για κάθε  . Θεωρούμε τη συνάρτηση
. Θεωρούμε τη συνάρτηση  με
με  . Τότε
. Τότε  . Άρα η
. Άρα η  είναι 1-1, συνεπώς το
είναι 1-1, συνεπώς το  είναι υπεραριθμήσιμο, άτοπο, γιατί
είναι υπεραριθμήσιμο, άτοπο, γιατί  . Άρα για κάποιο
. Άρα για κάποιο  το
το ![y_x \in [0,1]-\mathbb{Q} y_x \in [0,1]-\mathbb{Q}](/forum/ext/geomar/texintegr/latexrender/pictures/68131786b2896441d08bbed047c8ea71.png) , άρα
, άρα  , οπότε προφανώς
, οπότε προφανώς 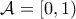 .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες