![f:[0, \frac{\pi}{2}] \rightarrow \mathbb{R} f:[0, \frac{\pi}{2}] \rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/cc5d7f599dbc3e5bc2e7a5ca6d7b06b9.png) συνεχής συνάρτηση. Να υπολογιστεί το όριο
συνεχής συνάρτηση. Να υπολογιστεί το όριο
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![h_{n}\in L^{1}\left ( \left [ 0,\frac{\pi }{2} \right ] \right ) h_{n}\in L^{1}\left ( \left [ 0,\frac{\pi }{2} \right ] \right )](/forum/ext/geomar/texintegr/latexrender/pictures/83078217aff2a016b72edcc5f04ec838.png) με
με  , όπου
, όπου 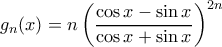 . Τώρα, μπορούμε να δείξουμε ότι αν
. Τώρα, μπορούμε να δείξουμε ότι αν ![x\in \left [ 0,\frac{\pi }{2} \right ] x\in \left [ 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/28d6a66842adb57a51ffdc6f088d39db.png) ισχύει
ισχύει  (απλό) επομένως αν
(απλό) επομένως αν ![x\in \left [ 0,\frac{\pi }{2} \right ] x\in \left [ 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/28d6a66842adb57a51ffdc6f088d39db.png) τότε
τότε  . Επίσης, αφού
. Επίσης, αφού  υπάρχει
υπάρχει 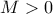 ώστε για κάθε
ώστε για κάθε  να ισχύει
να ισχύει  , για κάθε
, για κάθε ![x\in \left [ 0,\frac{\pi }{2} \right ] x\in \left [ 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/28d6a66842adb57a51ffdc6f088d39db.png) . Επομένως,
. Επομένως, 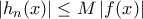 , για κάθε
, για κάθε ![x\in \left [ 0,\frac{\pi }{2} \right ] x\in \left [ 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/28d6a66842adb57a51ffdc6f088d39db.png) και η
και η  είναι ολοκληρώσιμη. Από θεώρημα κυριαρχημένης σύγκλισης έπεται ότι:
είναι ολοκληρώσιμη. Από θεώρημα κυριαρχημένης σύγκλισης έπεται ότι: ![\displaystyle{\lim_{n\rightarrow \infty }\int_{\left [ 0,\frac{\pi }{2} \right ]}h_{n}=\int_{\left [ 0,\frac{\pi }{2} \right ]}0=0} \displaystyle{\lim_{n\rightarrow \infty }\int_{\left [ 0,\frac{\pi }{2} \right ]}h_{n}=\int_{\left [ 0,\frac{\pi }{2} \right ]}0=0}](/forum/ext/geomar/texintegr/latexrender/pictures/a678fe804050f9e2956cfe5c46d3a8b8.png)
Τα παρακάτω δεν ισχύουνM.S.Vovos έγραψε: ↑Τετ Μάιος 19, 2021 2:36 pmΓεια σου Τόλη!
Θεωρώ την ακολουθίαμε
, όπου
. Τώρα, μπορούμε να δείξουμε ότι αν
ισχύει
(απλό) επομένως αν
τότε
. Επίσης, αφού
υπάρχει
ώστε για κάθε
να ισχύει
, για κάθε
. Επομένως,
, για κάθε
και η
είναι ολοκληρώσιμη. Από θεώρημα κυριαρχημένης σύγκλισης έπεται ότι:
Φιλικά,
Μάριος
Υ.Γ. Η συνέχεια δεν χρειάζεται μόνο η ολοκληρωσιμότητα. Ελπίζω να μην έχω κάνει κάποια πατάτα.
Υποπτευόμουν ότι δεν θα πάει καλά το συγκεκριμένο σημείο. Θα το ξαναδώ Σταύρο σε ευχαριστώ πολύ. Σώζεται με το θεώρημα κυριαρχημένης σύγκλισης ή θέλει ξήλωμα;
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες