Χρησιμοποιούμε το ολοκληρωτικό κριτήριο σύγκλισης:erxmer έγραψε:66) Ας υπολογιστεί το
Αν η
 είναι γνησίως φθίνουσα όπου
είναι γνησίως φθίνουσα όπου  ακέραιος, τότε
ακέραιος, τότε  για κάθε
για κάθε  .
.Έστω
 σταθερό μεγάλο.
σταθερό μεγάλο.Εκτιμούμε αρχικά το δεύτερο άθροισμα για
 σταθερό. Η
σταθερό. Η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  , άρα για
, άρα για  στο κριτήριο παίρνουμε
στο κριτήριο παίρνουμε 
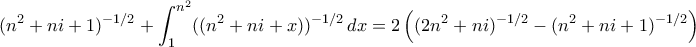 .
.Αθροίζουμε τις ανισότητες για
 και παίρνουμε
και παίρνουμε .
.Εφαρμόζουμε μια φορά ακόμα το κριτήριο για τις συναρτήσεις
 ,
,  στο
στο ![[1,n] [1,n]](/forum/ext/geomar/texintegr/latexrender/pictures/90d57222b4eae31784ea16305eec5305.png) για να πάρουμε το δεξί φράγμα και για τη συνάρτηση
για να πάρουμε το δεξί φράγμα και για τη συνάρτηση  στο ίδιο διάστημα για το αριστερό φράγμα, πολλαπλασιάζουμε με
στο ίδιο διάστημα για το αριστερό φράγμα, πολλαπλασιάζουμε με  , παίρνουμε όρια και από παρεμβολή
, παίρνουμε όρια και από παρεμβολή  .
.Το παραπάνω κριτήριο είναι πάρα πολύ χρήσιμο γιατί μπορούμε να περνάμε από άθροισμα σε ολοκλήρωμα που έχουμε μεγαλύτερη ελευθερία κινήσεων. Αν πχ κάπου σε μια παράσταση που ψάχνουμε όριο παρουσιάζεται μια σειρά
 που αποκλίνει, από το κριτήριο ξέρουμε ότι
που αποκλίνει, από το κριτήριο ξέρουμε ότι  , και το ολοκλήρωμα μπορεί ενδεχομένως να υπολογίζεται ή να μπορούμε ευκολότερα να εκτιμήσουμε τη συμπεριφορά του με ολοκλήρωση κατά μέρη ή άλλους τρόπους. Αυτά...
, και το ολοκλήρωμα μπορεί ενδεχομένως να υπολογίζεται ή να μπορούμε ευκολότερα να εκτιμήσουμε τη συμπεριφορά του με ολοκλήρωση κατά μέρη ή άλλους τρόπους. Αυτά...
 Ας υπολογισθεί, αν υπάρχει το όριο
Ας υπολογισθεί, αν υπάρχει το όριο  .
. Ας υπολογιστεί, αν υπάρχει, το όριο
Ας υπολογιστεί, αν υπάρχει, το όριο  .
.![\displaystyle{\mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{{\sqrt n }} \cdot \sqrt[{{n^2}}]{{\prod\limits_{i = 1}^n {{i^i}} }}} \right)} \displaystyle{\mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{{\sqrt n }} \cdot \sqrt[{{n^2}}]{{\prod\limits_{i = 1}^n {{i^i}} }}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/55988a6cdc9fd6d028f64ec5a2fcc2c9.png)
![\displaystyle{\sqrt[4]{e}} \displaystyle{\sqrt[4]{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/060fda4db8833392fac6e4684de48180.png)
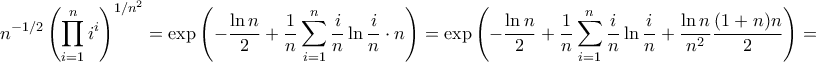
![\displaystyle{\sqrt[2n]{n}\exp\left(\frac{1}{n}\sum_{i=1}^{n}\frac{i}{n}\ln\frac{i}{n}\right)\to\exp\left(\int_{0}^{1}x\ln x\,dx\right)=e^{-1/4}} \displaystyle{\sqrt[2n]{n}\exp\left(\frac{1}{n}\sum_{i=1}^{n}\frac{i}{n}\ln\frac{i}{n}\right)\to\exp\left(\int_{0}^{1}x\ln x\,dx\right)=e^{-1/4}}](/forum/ext/geomar/texintegr/latexrender/pictures/8a080a8365200206585c1794b659525c.png) .
. δεν οριζεται οποτε παμε εψιλοντικα (lim ε->0). Το αποτελεσμα βεβαια δεν αλλαζει.
δεν οριζεται οποτε παμε εψιλοντικα (lim ε->0). Το αποτελεσμα βεβαια δεν αλλαζει. και το τελευταίο
και το τελευταίο και έτσι
και έτσι  .
. Υπολογίστε, αν υπάρχει, το όριο
Υπολογίστε, αν υπάρχει, το όριο  .
. και
και  θέση ολικού ελαχίστου της συνάρτησης
θέση ολικού ελαχίστου της συνάρτησης  , δηλαδή
, δηλαδή  . Τότε
. Τότε  .
. 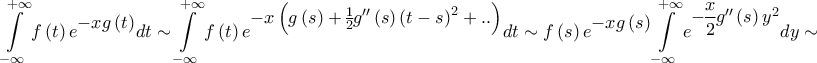

 και επειδή στην θέση
και επειδή στην θέση  έχουμε ολικό ελάχιστο για την
έχουμε ολικό ελάχιστο για την  ,
,  θα έχουμε
θα έχουμε 

 .
. Yπολογίστε το όριο
Yπολογίστε το όριο ![\displaystyle\lim_{n\rightarrow\infty}n\int_{0}^{\frac{\displaystyle\pi}{2}}{\left(1-\sqrt[n]{sinx}\right)dx} \displaystyle\lim_{n\rightarrow\infty}n\int_{0}^{\frac{\displaystyle\pi}{2}}{\left(1-\sqrt[n]{sinx}\right)dx}](/forum/ext/geomar/texintegr/latexrender/pictures/a6b046f7f56b4eecb928dddb53577b78.png) .
.![\displaystyle\lim_{n\rightarrow\infty}n\int_{0}^{\frac{\displaystyle\pi}{2}}{\left(1-\sqrt[n]{\sin x}\right)dx:=\lim_{n\to+\infty}\int_{0}^{\pi/2}f_{n}(x)\,dx} \displaystyle\lim_{n\rightarrow\infty}n\int_{0}^{\frac{\displaystyle\pi}{2}}{\left(1-\sqrt[n]{\sin x}\right)dx:=\lim_{n\to+\infty}\int_{0}^{\pi/2}f_{n}(x)\,dx}](/forum/ext/geomar/texintegr/latexrender/pictures/48dd58983bc47d2a8095d1107ccfcc95.png) .
.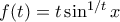 όπου
όπου ![x\in(0,\pi/2] x\in(0,\pi/2]](/forum/ext/geomar/texintegr/latexrender/pictures/236bc9c62634c3f44b9d0d451a230cf2.png) τυχαίο αλλά σταθερό και
τυχαίο αλλά σταθερό και  .
. 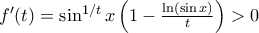 , άρα
, άρα  .
. για
για  , το οποίο έχουμε ξανασυζητήσει σε παλαιότερο ποστ ότι κάνει
, το οποίο έχουμε ξανασυζητήσει σε παλαιότερο ποστ ότι κάνει  .
.


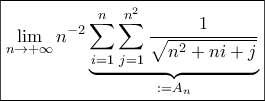
 Υπολογισθήτω το
Υπολογισθήτω το  .
.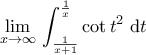
 στο
στο  , βλέπουμε ότι
, βλέπουμε ότι  άρα η
άρα η  συμπεριφέρεται κοντά στο
συμπεριφέρεται κοντά στο  . Κάνουμε λοιπόν το εξής για να απλουστεύσουμε την κατάσταση:
. Κάνουμε λοιπόν το εξής για να απλουστεύσουμε την κατάσταση: .
. , άρα
, άρα  ενώ
ενώ , άρα
, άρα  .
. κοντά στο
κοντά στο 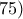 Αν
Αν 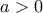 , ας βρεθεί αν υπάρχει το
, ας βρεθεί αν υπάρχει το 
 Να υπολογίσετε το όριο
Να υπολογίσετε το όριο 
 Να υπολογίσετε το όριο
Να υπολογίσετε το όριο 
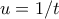 στο όριο και την
στο όριο και την  στο ολοκλήρωμα, ζητάμε να βρούμε το
στο ολοκλήρωμα, ζητάμε να βρούμε το  .
. ως συνεχής στο
ως συνεχής στο  θα έχει αρχική έστω
θα έχει αρχική έστω  με
με 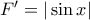 για
για  . Αυτή η
. Αυτή η 
 Η
Η  πάλι διότι η
πάλι διότι η 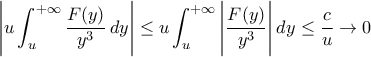 , άρα το δεξί πλευρικό είναι
, άρα το δεξί πλευρικό είναι