1)

2)

3)

με περιορισμούς
α)
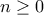
b)

Συντονιστές: grigkost, Κοτρώνης Αναστάσιος



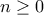

Tι ακριβώς εννοείς με την φράση "τις λύσεις"; Υποθέτω ότι εννοείς να βρούμε τον γενικό όρο σε κλειστή μορφή (άλλωστε μία είναι η μορφή οπότε ούτε ο πληθυντικός στο "λύσεις" χρειάζεται). Προχωρώ με αυτό κατά νου.
 . Θα δείξουμε με ισχυρή επαγωγή ότι
. Θα δείξουμε με ισχυρή επαγωγή ότι  . Πράγματι, για
. Πράγματι, για  ισχύει. Για το επαγωνικό βήμα υποθέτοντας ότι ισχύει για όλους τους
ισχύει. Για το επαγωνικό βήμα υποθέτοντας ότι ισχύει για όλους τους  έχουμε
έχουμε 
![= [\sin ((N+1)a) + \sin (N-1)a) ]-\sin ((N-1)a) = \sin ((N+1)a) = [\sin ((N+1)a) + \sin (N-1)a) ]-\sin ((N-1)a) = \sin ((N+1)a)](/forum/ext/geomar/texintegr/latexrender/pictures/9db67e3df2610bb4555d7d7c6787e946.png) , όπως θέλαμε.
, όπως θέλαμε.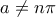 δεν χρειάστηκε.
δεν χρειάστηκε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες