Ασκήσεις Θεωρίας Μέτρου

stranger · #1

Έστω $\mu$ ένα εξωτερικό μέτρο σε ένα σύνολο

.
Έστω ότι για κάθε $S \subset X$ υπάρχει μετρήσιμο σύνολο

με $S \subset E$ και $\mu(S)=\mu(E)$ .
Έστω αύξουσα ακολουθία συνόλων (A_j)

(όχι κατ'ανάγκην μετρήσιμα).
Δείξτε ότι $\lim_{j \rightarrow \infty}\mu(A_j) = \mu(\cup_{n \in \mathbb{N}}A_n)$ .

stranger · #2

Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η

είναι Lipshitz με σταθερά

αν και μόνο αν είναι απόλυτα συνεχής και $|f^{\prime}(x)| \leq M$ σχεδόν παντού για

στο

.
Σημείωση: H

είναι Lipshitz με σταθερά

ανν $|f(x)-f(y)| \leq M|x-y|$ για κάθε x,y

.

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;

stranger · #3

Έστω συνάρτηση $f: [0,1] \rightarrow \mathbb{R}$ ολοκληρώσιμη(Lebesgue) στο [0,1]

.
Δείξτε ότι για κάθε $\epsilon >0$ υπάρχει $\delta >0$ ώστε για κάθε μετρήσιμο σύνολο $E \subset [0,1]$ με $\lambda(E) < \delta$ ισχύει $|\int_{E} f d \lambda| < \epsilon$ .
Εδώ $\lambda$ είναι το μέτρο Lebesgue.

sot arm · #4

Θα βάλω απάντηση σε κάποιες το βραδάκι καθώς δεν προλαβαίνω να γράψω σε λατεχ, απλα να αναφέρω σχετικά με αυτό:

stranger έγραψε: ↑
Δευ Νοέμ 09, 2020 11:32 pm

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;

Πως δεν υπάρχει τέτοια οικογένεια γενικά σε χώρο σ- πεπερασμένου μέτρου.

Από πού είναι οι ασκήσεις αν επιτρέπεται;

stranger · #5

sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 5:09 pm
Θα βάλω απάντηση σε κάποιες το βραδάκι καθώς δεν προλαβαίνω να γράψω σε λατεχ, απλα να αναφέρω σχετικά με αυτό:

stranger έγραψε: ↑
Δευ Νοέμ 09, 2020 11:32 pm

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;
Πως δεν υπάρχει τέτοια οικογένεια γενικά σε χώρο σ- πεπερασμένου μέτρου.

Από πού είναι οι ασκήσεις αν επιτρέπεται;

Οι περισσότερες είναι από διαγωνίσματα που έχω γράψει στη Θεωρία Μέτρου όσο ήμουνα φοιτητής(στην αμερική και στην ελλάδα).

stranger · #6

sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 5:09 pm
Θα βάλω απάντηση σε κάποιες το βραδάκι καθώς δεν προλαβαίνω να γράψω σε λατεχ, απλα να αναφέρω σχετικά με αυτό:

stranger έγραψε: ↑
Δευ Νοέμ 09, 2020 11:32 pm

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;
Πως δεν υπάρχει τέτοια οικογένεια γενικά σε χώρο σ- πεπερασμένου μέτρου.

Από πού είναι οι ασκήσεις αν επιτρέπεται;

Ίσως δεν βλέπω κάτι. Τα σύνολα πρέπει να είναι ξένα ανά δυο και υπεραριθμήσιμα το πλήθος. Πιο αναλυτικά;

stranger · #7

ΛΑΘΟΣ

sot arm · #8

Συμπληρώνω αυτό που έλεγα προηγουμένως, συγκεκριμένα έστω: $( X , \mathcal{M}, \mu )$ χώρος σ - πεπερασμένου μέτρου
και $\{A_{i} \} , i \in I$ οικογένεια ξένων ανά δύο υποσυνόλων της $\mathcal{M}$ θετικού μέτρου, θα δείξω πως το

είναι το πολύ αριθμήσιμο.

Αφού ο $( X , \mathcal{M}, \mu )$ είναι χώρος σ - πεπερασμένου μέτρου υπάρχουν $\{E_{k}\}_{k \in \mathbb{N}}$ θετικού πεπερασμένου μέτρου
με $\displaystyle{ \bigcup_{k=1}^{\infty}E_{k} = X }$ .

Θέτουμε: $I_{n}= \bigcup_{k=1}^{n}E_{k}$ τότε η $I_{n}$ είναι αύξουσα ακολουθία συνόλων και η αριθμήσιμη άπειρη ένωση τους καλύπτει τον

. Αν το

είναι υπεραριθμήσιμο υπάρχει κάποιος δείκτης

έτσι ώστε υπεραριθμήσιμα το πλήθος εκ των $A_{i}$ να περιέχονται στο $I_{N}$ .

Έστω τώρα $J_{N,n} = \{ A_{i} , i \in I : A_{i} \subset I_{N} , \mu(A_{i}) \geq \frac{1}{k} \}$ . Τότε εμφανώς το σύνολο: $\bigcup_{k=1}^{\infty}J_{N,k}$ περιέχει όλα τα $A_{i}$ που περιέχονται στο $I_{N}$ , άρα κάποιο εκ των $J_{N,k}$ υπεραριθμήσιμο.

Αυτό είναι άτοπο καθώς το πλήθος τους μπορεί να είναι το πολύ $\mu(I_{N}) k$ αφού είναι ξένα ανά δύο , άρα το ζητούμενο έχει δειχθεί.

edit- συμπλήρωση: μπορούμε να πούμε το ίδιο στην περίπτωση όπου έχουμε ξένα ανά δύο υποσύνολα με θετικό εξωτερικό μέτρο;
Δηλαδή δεν υποθέτω την μετρησιμότητα που χρησιμοποιήθηκε στο τελευταίο βήμα

edit 2 : Υπάρχει λάθος , συμπληρώνω από κάτω τις λεπτομέριες, ευχαριστώ τον κύριο Σταύρο που το παρατήρησε.

stranger · #9

sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 8:58 pm
Συμπληρώνω αυτό που έλεγα προηγουμένως, συγκεκριμένα έστω: $( X , \mathcal{M}, \mu )$ χώρος σ - πεπερασμένου μέτρου
και $\{A_{i} \} , i \in I$ οικογένεια ξένων ανά δύο υποσυνόλων της $\mathcal{M}$ θετικού μέτρου, θα δείξω πως το είναι το πολύ αριθμήσιμο.

Αφού ο $( X , \mathcal{M}, \mu )$ είναι χώρος σ - πεπερασμένου μέτρου υπάρχουν $\{E_{k}\}_{k \in \mathbb{N}}$ θετικού πεπερασμένου μέτρου
με $\displaystyle{ \bigcup_{k=1}^{\infty}E_{k} = X }$ .

Θέτουμε: $I_{n}= \bigcup_{k=1}^{n}E_{k}$ τότε η $I_{n}$ είναι αύξουσα ακολουθία συνόλων και η αριθμήσιμη άπειρη ένωση τους καλύπτει τον . Αν το είναι υπεραριθμήσιμο υπάρχει κάποιος δείκτης έτσι ώστε υπεραριθμήσιμα το πλήθος εκ των $A_{i}$ να περιέχονται στο $I_{N}$ .

Έστω τώρα $J_{N,n} = \{ A_{i} , i \in I : A_{i} \subset I_{N} , \mu(A_{i}) \geq \frac{1}{k} \}$ . Τότε εμφανώς το σύνολο: $\bigcup_{k=1}^{\infty}J_{N,k}$ περιέχει όλα τα $A_{i}$ που περιέχονται στο $I_{N}$ , άρα κάποιο εκ των $J_{N,k}$ υπεραριθμήσιμο.

Αυτό είναι άτοπο καθώς το πλήθος τους μπορεί να είναι το πολύ $\mu(I_{N}) k$ αφού είναι ξένα ανά δύο , άρα το ζητούμενο έχει δειχθεί.

edit- συμπλήρωση: μπορούμε να πούμε το ίδιο στην περίπτωση όπου έχουμε ξένα ανά δύο υποσύνολα με θετικό εξωτερικό μέτρο;
Δηλαδή δεν υποθέτω την μετρησιμότητα που χρησιμοποιήθηκε στο τελευταίο βήμα.

Είσαι σωστός και μερακλής!

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #10

sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 8:58 pm
Συμπληρώνω αυτό που έλεγα προηγουμένως, συγκεκριμένα έστω: $( X , \mathcal{M}, \mu )$ χώρος σ - πεπερασμένου μέτρου
και $\{A_{i} \} , i \in I$ οικογένεια ξένων ανά δύο υποσυνόλων της $\mathcal{M}$ θετικού μέτρου, θα δείξω πως το είναι το πολύ αριθμήσιμο.

Αφού ο $( X , \mathcal{M}, \mu )$ είναι χώρος σ - πεπερασμένου μέτρου υπάρχουν $\{E_{k}\}_{k \in \mathbb{N}}$ θετικού πεπερασμένου μέτρου
με $\displaystyle{ \bigcup_{k=1}^{\infty}E_{k} = X }$ .

Θέτουμε: $I_{n}= \bigcup_{k=1}^{n}E_{k}$ τότε η $I_{n}$ είναι αύξουσα ακολουθία συνόλων και η αριθμήσιμη άπειρη ένωση τους καλύπτει τον . Αν το είναι υπεραριθμήσιμο υπάρχει κάποιος δείκτης έτσι ώστε υπεραριθμήσιμα το πλήθος εκ των $A_{i}$ να περιέχονται στο $I_{N}$ .

Έστω τώρα $J_{N,n} = \{ A_{i} , i \in I : A_{i} \subset I_{N} , \mu(A_{i}) \geq \frac{1}{k} \}$ . Τότε εμφανώς το σύνολο: $\bigcup_{k=1}^{\infty}J_{N,k}$ περιέχει όλα τα $A_{i}$ που περιέχονται στο $I_{N}$ , άρα κάποιο εκ των $J_{N,k}$ υπεραριθμήσιμο.

Αυτό είναι άτοπο καθώς το πλήθος τους μπορεί να είναι το πολύ $\mu(I_{N}) k$ αφού είναι ξένα ανά δύο , άρα το ζητούμενο έχει δειχθεί.

edit- συμπλήρωση: μπορούμε να πούμε το ίδιο στην περίπτωση όπου έχουμε ξένα ανά δύο υποσύνολα με θετικό εξωτερικό μέτρο;
Δηλαδή δεν υποθέτω την μετρησιμότητα που χρησιμοποιήθηκε στο τελευταίο βήμα.

Γεια σου Σωτήρη.
Το παρακάτω δεν ισχύει

sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 8:58 pm
Θέτουμε: $I_{n}= \bigcup_{k=1}^{n}E_{k}$ τότε η $I_{n}$ είναι αύξουσα ακολουθία συνόλων και η αριθμήσιμη άπειρη ένωση τους καλύπτει τον . Αν το είναι υπεραριθμήσιμο υπάρχει κάποιος δείκτης έτσι ώστε υπεραριθμήσιμα το πλήθος εκ των $A_{i}$ να περιέχονται στο $I_{N}$ .

Μπορεί και κανένα να μην περιέχεται.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #11

stranger έγραψε: ↑
Δευ Νοέμ 09, 2020 11:32 pm
Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η είναι Lipshitz με σταθερά αν και μόνο αν είναι απόλυτα συνεχής και $f^{\prime}(x) \leq M$ σχεδόν παντού για στο .
Σημείωση: H είναι Lipshitz με σταθερά ανν $|f(x)-f(y)| \leq M|x-y|$ για κάθε .

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;

το
Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η

είναι Lipshitz με σταθερά

αν και μόνο αν είναι απόλυτα συνεχής και $f^{\prime}(x) \leq M$ σχεδόν παντού για

στο

.
δεν ισχύει.
π.χ πάρε $f:[0,1]\rightarrow \mathbb{R},f(x)=-\sqrt{x}$
Διορθώνεται βέβαια.

stranger · #12

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Νοέμ 10, 2020 10:57 pm

stranger έγραψε: ↑
Δευ Νοέμ 09, 2020 11:32 pm
Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η είναι Lipshitz με σταθερά αν και μόνο αν είναι απόλυτα συνεχής και $f^{\prime}(x) \leq M$ σχεδόν παντού για στο .
Σημείωση: H είναι Lipshitz με σταθερά ανν $|f(x)-f(y)| \leq M|x-y|$ για κάθε .

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;
το
Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η είναι Lipshitz με σταθερά αν και μόνο αν είναι απόλυτα συνεχής και $f^{\prime}(x) \leq M$ σχεδόν παντού για στο .
δεν ισχύει.
π.χ πάρε $f:[0,1]\rightarrow \mathbb{R},f(x)=-\sqrt{x}$
Διορθώνεται βέβαια.

Νομίζω πως κάνεις λάθος. H $-\sqrt{x}$ δεν είναι Lipshitz.

sot arm · #13

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Νοέμ 10, 2020 10:52 pm

sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 8:58 pm
Συμπληρώνω αυτό που έλεγα προηγουμένως, συγκεκριμένα έστω: $( X , \mathcal{M}, \mu )$ χώρος σ - πεπερασμένου μέτρου
και $\{A_{i} \} , i \in I$ οικογένεια ξένων ανά δύο υποσυνόλων της $\mathcal{M}$ θετικού μέτρου, θα δείξω πως το είναι το πολύ αριθμήσιμο.

Αφού ο $( X , \mathcal{M}, \mu )$ είναι χώρος σ - πεπερασμένου μέτρου υπάρχουν $\{E_{k}\}_{k \in \mathbb{N}}$ θετικού πεπερασμένου μέτρου
με $\displaystyle{ \bigcup_{k=1}^{\infty}E_{k} = X }$ .

Θέτουμε: $I_{n}= \bigcup_{k=1}^{n}E_{k}$ τότε η $I_{n}$ είναι αύξουσα ακολουθία συνόλων και η αριθμήσιμη άπειρη ένωση τους καλύπτει τον . Αν το είναι υπεραριθμήσιμο υπάρχει κάποιος δείκτης έτσι ώστε υπεραριθμήσιμα το πλήθος εκ των $A_{i}$ να περιέχονται στο $I_{N}$ .

Έστω τώρα $J_{N,n} = \{ A_{i} , i \in I : A_{i} \subset I_{N} , \mu(A_{i}) \geq \frac{1}{k} \}$ . Τότε εμφανώς το σύνολο: $\bigcup_{k=1}^{\infty}J_{N,k}$ περιέχει όλα τα $A_{i}$ που περιέχονται στο $I_{N}$ , άρα κάποιο εκ των $J_{N,k}$ υπεραριθμήσιμο.

Αυτό είναι άτοπο καθώς το πλήθος τους μπορεί να είναι το πολύ $\mu(I_{N}) k$ αφού είναι ξένα ανά δύο , άρα το ζητούμενο έχει δειχθεί.

edit- συμπλήρωση: μπορούμε να πούμε το ίδιο στην περίπτωση όπου έχουμε ξένα ανά δύο υποσύνολα με θετικό εξωτερικό μέτρο;
Δηλαδή δεν υποθέτω την μετρησιμότητα που χρησιμοποιήθηκε στο τελευταίο βήμα.
Γεια σου Σωτήρη.
Το παρακάτω δεν ισχύει
sot arm έγραψε: ↑
Τρί Νοέμ 10, 2020 8:58 pm
Θέτουμε: $I_{n}= \bigcup_{k=1}^{n}E_{k}$ τότε η $I_{n}$ είναι αύξουσα ακολουθία συνόλων και η αριθμήσιμη άπειρη ένωση τους καλύπτει τον . Αν το είναι υπεραριθμήσιμο υπάρχει κάποιος δείκτης έτσι ώστε υπεραριθμήσιμα το πλήθος εκ των $A_{i}$ να περιέχονται στο $I_{N}$ .
Μπορεί και κανένα να μην περιέχεται.

Γεια σας , πιθανώς να χάνω κάτι, αλλά δεν το βλέπω.

Έχετε αντιπαράδειγμα;

Edit: έχετε δίκιο , το είδα γιατί το φτιαχνω το κομμάτι και επανέρχομαι.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #14

stranger έγραψε: ↑
Τρί Νοέμ 10, 2020 11:13 pm

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Νοέμ 10, 2020 10:57 pm

stranger έγραψε: ↑
Δευ Νοέμ 09, 2020 11:32 pm
Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η είναι Lipshitz με σταθερά αν και μόνο αν είναι απόλυτα συνεχής και $f^{\prime}(x) \leq M$ σχεδόν παντού για στο .
Σημείωση: H είναι Lipshitz με σταθερά ανν $|f(x)-f(y)| \leq M|x-y|$ για κάθε .

Υπάρχει υπεραριθμήσιμη οικογένεια ξένων ανά δυο υποσυνόλων του $\mathbb{R}$ που το καθένα από αυτά έχει θετικό μέτρο Lebesgue;
το
Έστω $f:[0,1] \rightarrow \mathbb{R}$ .
Δείξτε ότι η είναι Lipshitz με σταθερά αν και μόνο αν είναι απόλυτα συνεχής και $f^{\prime}(x) \leq M$ σχεδόν παντού για στο .
δεν ισχύει.
π.χ πάρε $f:[0,1]\rightarrow \mathbb{R},f(x)=-\sqrt{x}$
Διορθώνεται βέβαια.
Νομίζω πως κάνεις λάθος. H $-\sqrt{x}$ δεν είναι Lipshitz.

Φυσικά και δεν είναι .
Είναι όμως απολύτως συνεχής και $f^{\prime}(x) \leq M$
για M=1

π.χ

stranger · #15

Α τώρα το είδα αυτό που λες. έχω ξεχάσει να βάλω απόλυτο.
Σε ευχαριστώ.
edit. Η σωστή εκφώνηση είναι $|f^{\prime}(x)| \leq M$ και όχι $f^{\prime}(x) \leq M$ .

sot arm · #16

Επανέρχομαι λοιπόν , μπορούμε να θέσουμε διαφορετικά:

$\displaystyle{I_{n} = \{ i \in I : \mu(A_{i} \bigcap E_{n}) > 0 \}}$

Τότε $I = \bigcup_{n\in \mathbb{N} }I_{n}$ αφού για κάθε $A_{i}$ έχουμε $\lim_{n\rightarrow +\infty} \mu(A_{i}\bigcap \bigcup_{k=1}^{n}E_{k}) = \mu(A_{i}}) > 0$ από την συνέχεια από κάτω του μέτρου.

Το υπόλοιπο επιχείρημα περνάει ατόφιο αφού θα υπάρχει κάποιο $I_{n}$ με υπεραριθμήσιμο το πλήθος δείκτες

και ορίζουμε τα $J_{N,k}$ όπως πριν με την διαφορά ότι θέλουμε:

$\displaystyle{ J_{N,k}= \{ i \in I , \mu(A_{i} \cap I_{N}) \geq \frac{1}{k}\}}$

stranger · #17

ΛΑΘΟΣ.

stranger · #18

Υπολογίστε το $\int_{0}^{\infty} \frac{1}{x^4+1} dx$ .
Υπόδειξη: Μιγαδική Ανάλυση

stranger · #19

stranger έγραψε: ↑
Τρί Νοέμ 10, 2020 5:03 pm
Έστω συνάρτηση $f: [0,1] \rightarrow \mathbb{R}$ ολοκληρώσιμη(Lebesgue) στο .
Δείξτε ότι για κάθε $\epsilon >0$ υπάρχει $\delta >0$ ώστε για κάθε μετρήσιμο σύνολο $E \subset [0,1]$ με $\lambda(E) < \delta$ ισχύει $|\int_{E} f d \lambda| < \epsilon$ .
Εδώ $\lambda$ είναι το μέτρο Lebesgue.

Εις άτοπον.
Έστω ότι υπάρχει $\epsilon >0$ ώστε για κάθε $\delta>0$ υπάρχει μετρήσιμο σύνολο

με $\lambda(E)<\delta$ και $\int_{E}|f| d\lambda \geq \epsilon$ .
Για κάθε $n \in \mathbb{N}$ επιλέγουμε σύνολο E_n

μετρήσιμο με $\lambda(E_n)< \frac{1}{n^2}$ και $\int_{E_n}|f|d \lambda \geq \epsilon$ .
Έστω το σύνολο $E= \cap_{n=1}^{\infty} \cup_{k=n}^{\infty}E_k$ .
Τότε το

είναι μετρήσιμο και $\lambda(E) \leq \lambda(\cup_{k=n}^{\infty}E_k)$ για κάθε $n \in \mathbb{N}$ .
Όμως $\lambda(\cup_{k=n}^{\infty}E_k) \leq \sum_{k=n}^{\infty} \lambda(E_k) \leq \sum_{k=n}^{\infty}\frac{1}{k^2} \rightarrow 0$ όταν $n \rightarrow \infty$ .
Άρα $\lambda(E)=0$ . Επίσης το $F \rightarrow \int_{F}|f| d\lambda$ είναι μέτρο.
Άρα αφού η

είναι ολοκληρώσιμη έχουμε $\int_E |f| d\lambda = \lim_{n \rightarrow \infty}\int_{\cup_{k=n}^{\infty} E_k}|f| d \lambda \geq \limsup_{n \rightarrow \infty}\int_{E_n} |f| d\lambda \geq \epsilon$ .
Όμως $\int_{E} |f| d \lambda = 0$ επειδή $\lambda(E)=0$ το οποίο φέρνει το άτοπο.
Άρα τελικά $\forall \epsilon>0 \exists \delta>0 : \forall E \lambda(E)<\delta \implies |\int_{E}f d \lambda| \leq \int_{E}|f| d \lambda < \epsilon$ .

#20

stranger έγραψε: ↑
Τετ Νοέμ 11, 2020 3:04 pm
Υπολογίστε το $\int_{0}^{\infty} \frac{1}{x^4+1} dx$ .
Υπόδειξη: Μιγαδική Ανάλυση

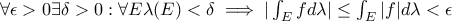Δεν είναι η θέση της σε θρεντ Θεωρίας Μέτρου, ούτε η Μιγαδική Ανάλυση (όπως λέει η υπόδειξη) είναι απαραίτητη. Θα δείξω τρόπο χωρίς Μιγαδική διότι με Μιγαδική το εν λόγω παράδειγμα υπάρχει σε όλα τα σχετικά βιβλία, συχνά λυμένο.

Η αλλαγή μεταβλητής y=1/x

δείχνει ότι το δοθέν ολοκλήρωμα

ικανοποιεί

$\displaystyle{I= \int_{0}^{\infty} \frac{x^2}{x^4+1} dx}$ . Άρα

$\displaystyle{2I = \int_{0}^{\infty} \frac{x^2+1}{x^4+1} dx= \int_{0}^{\infty} \frac{x^2-\sqrt 2x+ 1}{x^4+1} dx +\sqrt 2 \int_{0}^{\infty} \frac{ x}{x^4+1} dx}$

$\displaystyle{ = \int_{0}^{\infty} \frac{1}{x^2-\sqrt 2x+ 1 } dx +\sqrt 2 \int_{0}^{\infty} \frac{ x}{x^4+1} dx}$

Τώρα το μεν πρώτο είναι άμεσο με τόξο εφαπτομένης και το δεύτερο με την αλλαγή μεταβλητής y=x^2

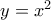. Τα αφήνω ως άμεσα και γνωστά.

Ασκήσεις Θεωρίας Μέτρου

Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Re: Ασκήσεις Θεωρίας Μέτρου

Μέλη σε σύνδεση