Ίσως είναι προφανές αλλά το κεφάλι μου έχει πραγματικά διαλυθεί από τον προγραμματισμό.
Ισχύει το κάτωθι ?
 όπου
όπου  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 όπου
όπου  .
.Αν και δεν μας λες τι ακριβώς είναι τα εν λόγω σύμβολα, δεν φαίνεται να ισχύει για προφανείς λόγους. Π.χ. ανsokratis lyras έγραψε: ↑Τρί Αύγ 11, 2020 3:20 pmΚαλησπέρα,
Ίσως είναι προφανές αλλά το κεφάλι μου έχει πραγματικά διαλυθεί από τον προγραμματισμό.
Ισχύει το κάτωθι ?
όπου
.
 και
και  , τότε το αριστερό μέλος είναι
, τότε το αριστερό μέλος είναι  , ενώ το δεξί
, ενώ το δεξί  .
. Συγγνώμη, ξέχασα να αναφέρω τον περιορισμόMihalis_Lambrou έγραψε: ↑Τρί Αύγ 11, 2020 3:37 pmΑν και δεν μας λες τι ακριβώς είναι τα εν λόγω σύμβολα, δεν φαίνεται να ισχύει για προφανείς λόγους. Π.χ. ανsokratis lyras έγραψε: ↑Τρί Αύγ 11, 2020 3:20 pmΚαλησπέρα,
Ίσως είναι προφανές αλλά το κεφάλι μου έχει πραγματικά διαλυθεί από τον προγραμματισμό.
Ισχύει το κάτωθι ?
όπου
.
και
, τότε το αριστερό μέλος είναι
, ενώ το δεξί
.
Χάνω κάτι;
 .
.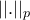 ειναι η συνήθης p-norm του
ειναι η συνήθης p-norm του  και στο σημείο
και στο σημείο  εννοώ την νόρμα πινάκων που ορίζει η
εννοώ την νόρμα πινάκων που ορίζει η 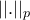 .
.Δεν το σώζει αυτό. Πάρε π.χ.
 αλλά
αλλά  πολύ κοντά στο
πολύ κοντά στο  . Ακριβέστερα, για
. Ακριβέστερα, για  πάρε ακολουθία
πάρε ακολουθία  . Τότε το αριστερό μέλος για τα
. Τότε το αριστερό μέλος για τα  που έγραψα τείνει στο
που έγραψα τείνει στο  (πριν ήταν ακριβώς ίσο με το
(πριν ήταν ακριβώς ίσο με το  ) ενώ το δεξί τείνει το
) ενώ το δεξί τείνει το  (πριν ήταν ακριβώς ίσο με
(πριν ήταν ακριβώς ίσο με  ). Πάλι αντίφαση.
). Πάλι αντίφαση. , μία piecewise linear συνάρτηση είναι Lipschitz με σταθερά Lipschitz τη μεγαλύτερη, κατά απόλυτη τιμή, κλίση που έχει σε κάποιο κομμάτι της και ήθελα να γενικεύσω το αποτέλεσμα αυτό στις πολλές διαστάσεις, όπου piecewise linear στο
, μία piecewise linear συνάρτηση είναι Lipschitz με σταθερά Lipschitz τη μεγαλύτερη, κατά απόλυτη τιμή, κλίση που έχει σε κάποιο κομμάτι της και ήθελα να γενικεύσω το αποτέλεσμα αυτό στις πολλές διαστάσεις, όπου piecewise linear στο ![[a, b]^d [a, b]^d](/forum/ext/geomar/texintegr/latexrender/pictures/ac9cf3e200c94df776e534253d1d704d.png) θεωρώ κάθε συνάρτηση ορισμένη στο
θεωρώ κάθε συνάρτηση ορισμένη στο ![[a, b]^d [a, b]^d](/forum/ext/geomar/texintegr/latexrender/pictures/5141fa1cda28770fa5298a0a871baa87.png) που απαρτίζεται από πεπερασμένα τω πλήθος 'κομμάτια' της μορφής
που απαρτίζεται από πεπερασμένα τω πλήθος 'κομμάτια' της μορφής 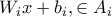 , όπου τα
, όπου τα  αποτελούν μια πεπερασμένη διαμέριση του
αποτελούν μια πεπερασμένη διαμέριση του ![[a, b]^d [a, b]^d](/forum/ext/geomar/texintegr/latexrender/pictures/ac9cf3e200c94df776e534253d1d704d.png) .
. .
. Δεν ξέρω να απαντήσω στο τελευταίο σου ποστ (κυρίως δεν καταλαβαίνω τι ρωτάς) αλλά ας δούμε και άλλον έναν λόγοsokratis lyras έγραψε: ↑Τρί Αύγ 11, 2020 3:20 pmΚαλησπέρα,
Ίσως είναι προφανές αλλά το κεφάλι μου έχει πραγματικά διαλυθεί από τον προγραμματισμό.
Ισχύει το κάτωθι ?
όπου
.
 . Τότε το ζητούμενο γίνεται
. Τότε το ζητούμενο γίνεται 
 στο αριστερό μέλος, πλην όμως μπορούμε να βάλουμε οποιοδήποτε
στο αριστερό μέλος, πλην όμως μπορούμε να βάλουμε οποιοδήποτε  στο δεξί. Εεεε, δεν γίνεται! Μάλιστα, το μόνο
στο δεξί. Εεεε, δεν γίνεται! Μάλιστα, το μόνο  για το οποίο ισχύει η ανισότητα είναι το
για το οποίο ισχύει η ανισότητα είναι το 
Δεν ξέρω αν χάνω κάτι αλλά νομίζω ότι είναι απλό.sokratis lyras έγραψε: ↑Τετ Αύγ 12, 2020 2:06 pmΣτην ουσία ρωτάω αυτό: https://math.stackexchange.com/questio ... -in-bbb-rd.
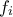 τους περιορισμούς της
τους περιορισμούς της 

 στα
στα 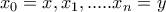
 είναι στο ίδιο
είναι στο ίδιο 

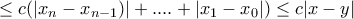
 είναι το μέγιστο από τις σταθερές κάθε
είναι το μέγιστο από τις σταθερές κάθε 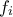 .
.Δεν καταλαβαίνω γιατί ισχύει η τελευταία ανισότητα.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Αύγ 12, 2020 10:58 pmΔεν ξέρω αν χάνω κάτι αλλά νομίζω ότι είναι απλό.sokratis lyras έγραψε: ↑Τετ Αύγ 12, 2020 2:06 pmΣτην ουσία ρωτάω αυτό: https://math.stackexchange.com/questio ... -in-bbb-rd.
Συμβολίζω μετους περιορισμούς της
Εστω
Θεωρούμε την ευθεία που περνάει από αυτά και τέμνει τα διάφοραστα
Εχουμε ότι ταείναι στο ίδιο
Τότε
Η σταθεράείναι το μέγιστο από τις σταθερές κάθε
.
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες