Σελίδα 1 από 1
Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Τρί Ιούλ 14, 2020 9:58 pm
από Tolaso J Kos
Re: Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Τρί Ιούλ 14, 2020 11:07 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 9:58 pm
Έστω

.
- Χρησιμοποιώντας το extended binomial theorem αναπτύξτε τη συνάρτηση
 σε σειρά Fourier συνημιτόνων.
σε σειρά Fourier συνημιτόνων.
- Να δειχθεί η ταυτότητα:
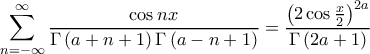
όπου  η συνάρτηση Γάμμα του Euler.
η συνάρτηση Γάμμα του Euler.
Τόλη γράψε σωστά την εκφώνηση.
Πχ τι είναι το

;
Για ποία

ισχύει η ταυτότητα.
Re: Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Τρί Ιούλ 14, 2020 11:10 pm
από Tolaso J Kos
Μα Σταύρο στο ορίζω το

. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα

.
Re: Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Τρί Ιούλ 14, 2020 11:49 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pm
Μα Σταύρο στο ορίζω το

. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα

.
Δεν το είδα.
Και ο λόγος είναι γιατί τότε πρέπει να περιορίσεις τα

Η ταυτότητα αποκλείεται να ισχύει στο

.
Πρόσεξε το

δεν οριζεται στο

και στο

δεν είναι μονοσήμαντα ορισμένο.
Re: Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Τετ Ιούλ 15, 2020 8:51 am
από Mihalis_Lambrou
Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 9:58 pm
Έστω

.
- Χρησιμοποιώντας το extended binomial theorem αναπτύξτε τη συνάρτηση
 σε σειρά Fourier συνημιτόνων.
σε σειρά Fourier συνημιτόνων.
- Να δειχθεί η ταυτότητα:
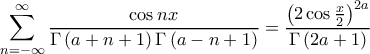
όπου  η συνάρτηση Γάμμα του Euler.
η συνάρτηση Γάμμα του Euler.
Σίγουρα;
Πέρα από το σχόλιο του Σταύρου, έχω και άλλες απορίες: Μήπως το

πρέπει να γίνει

(αλλά τότε δεν είναι σειρά Fourier).
Επίσης, σίγουρα το άθροισμα πάει από "μείον άπειρο στο άπειρο" και όχι από το "μηδέν στο άπειρο"; Έχω δύο λόγους να το νομίζω αυτό. Ο πρώτος είναι ότι αν πούμε

τον τυπικό συντελεστή τότε

οπότε φεύγουν κατά ζεύγη και μένει μόνο ο όρος
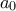
.
Άλλος λόγος είναι ότι στο πρώτο ερώτημα έχουμε, εκεί που έχει νόημα η παράσταση,

H παράσταση αυτή οδηγεί σε ταυτότητα που μοιάζει με την ζητούμενη αλλά δεν είναι ακριβώς ίδια (οι συντελεστές έχουν μικροδιαφορές και το

είναι σε δυνάμεις).
Μήπως δεν βλέπω κάτι γιατί... δεν ήπια ακόμη καφέ;
Re: Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Τετ Ιούλ 15, 2020 10:17 am
από Tolaso J Kos
Η ταυτότητα έχει ελεγχθεί με το W|A για διάφορες τιμές των

και

. Είναι:

Οπότε,

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 14, 2020 11:49 pm
Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pm
Μα Σταύρο στο ορίζω το

. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα

.
Δεν το είδα.
Και ο λόγος είναι γιατί τότε πρέπει να περιορίσεις τα

Η ταυτότητα αποκλείεται να ισχύει στο

.
Πρόσεξε το

δεν οριζεται στο

και στο

δεν είναι μονοσήμαντα ορισμένο.
Ας βάλουμε για τα

που ορίζεται.
Extended Binomial Theorem έγραψε:
Re: Ανάπτυγμα Fourier συνημιτόνων
Δημοσιεύτηκε: Παρ Ιούλ 17, 2020 9:44 am
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Tolaso J Kos έγραψε: ↑Τετ Ιούλ 15, 2020 10:17 am
Η ταυτότητα έχει ελεγχθεί με το W|A για διάφορες τιμές των

και

. Είναι:

Οπότε,

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 14, 2020 11:49 pm
Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pm
Μα Σταύρο στο ορίζω το

. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα

.
Δεν το είδα.
Και ο λόγος είναι γιατί τότε πρέπει να περιορίσεις τα

Η ταυτότητα αποκλείεται να ισχύει στο

.
Πρόσεξε το

δεν οριζεται στο

και στο

δεν είναι μονοσήμαντα ορισμένο.
Ας βάλουμε για τα

που ορίζεται.
Extended Binomial Theorem έγραψε:
Καλημέρα από την Χαλκίδα.
Τουλάχιστον για μένα υπάρχουν πολλά προβλήματα.
Μερικά από αυτά είναι
Extended Binomial Theorem έγραψε:
Από ότι είδα στην παραπομπή ο τύπος ισχύει για μιγαδικά

Αλλά είναι γνωστό ότι δύναμη μιγαδικού σε μιγαδικό γενικά δεν ορίζεται μονοσήμαντα.
Αυτό σημαίνει ότι για να ισχύει ο τύπος πρέπει να γίνουν κάποιες παραδοχές που δεν αναφέρονται
και φυσικά δεν τις γνωρίζω.
Η συνάρτηση

έχει πόλους.
Τι γίνεται όταν στον παρανομαστή έχουμε

;
Το βάζουμε

;
Η συνάρτηση που ζητείται να αναπτυχθεί σε σειρά Fourier δεν είναι πάντα ολοκληρώσιμη.
Ετσι δεν μπορούμε να έχουμε σειρά Fourier- Lebesgue.
Μπορεί όμως να έχουμε σειρά Fourier- Riemman.
Ο υπολογισμός που έγραψες είναι καθαρά τυπικός και σίγουρα για να ισχύει πρέπει να γίνουν κάποιες
παραδοχές.
Tolaso J Kos έγραψε: ↑Τετ Ιούλ 15, 2020 10:17 am
Ας βάλουμε για τα

που ορίζεται.
Νομίζω ότι θα χάσουμε την μπάλα.
Και υπάρχει το πρόβλημα των ορισμών που θα δεχθούμε.
Ερωτήσεις για τον Τόλη.
1.Από που είναι το θέμα ;
2.Εχεις λινκ με την απόδειξη του Exteded Binomial Theorem ;
 .
.  .
.  σε σειρά Fourier συνημιτόνων.
σε σειρά Fourier συνημιτόνων.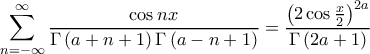
 η συνάρτηση Γάμμα του Euler.
η συνάρτηση Γάμμα του Euler. ;
; ισχύει η ταυτότητα.
ισχύει η ταυτότητα. .
. .
.

 πρέπει να γίνει
πρέπει να γίνει  (αλλά τότε δεν είναι σειρά Fourier).
(αλλά τότε δεν είναι σειρά Fourier).  τον τυπικό συντελεστή τότε
τον τυπικό συντελεστή τότε 
 .
.
 είναι σε δυνάμεις).
είναι σε δυνάμεις). 

 που ορίζεται.
που ορίζεται.

 ;
; ;
;