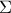 το στερεό που περικλείεται από το μονόχωνο υπερβολοειδές
το στερεό που περικλείεται από το μονόχωνο υπερβολοειδές  και το δίχωνο υπερβολοειδές
και το δίχωνο υπερβολοειδές  .
. Να βρεθεί ο όγκος του
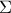 συναρτήσει των
συναρτήσει των  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
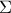 το στερεό που περικλείεται από το μονόχωνο υπερβολοειδές
το στερεό που περικλείεται από το μονόχωνο υπερβολοειδές  και το δίχωνο υπερβολοειδές
και το δίχωνο υπερβολοειδές  .
. 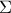 συναρτήσει των
συναρτήσει των  .
.
 των αρχικών επιφανειών
των αρχικών επιφανειώνΚαλησπέρα...
 παρουσιάζω το κατωτέρω σχήμα:
παρουσιάζω το κατωτέρω σχήμα: ...για όσους ενδιαφέρονται, επιπρόσθετα:
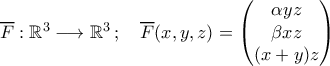
 , όπου
, όπου  το μονόχωνο υπερβολοειδές.
το μονόχωνο υπερβολοειδές.
Γρηγόρη καλημέρα....
 του αρχικού στερεού.
Στο δεύτερο σχήμα εμφανίζεται ένα τμήμα κυλινδρικης επιφάνειας
του αρχικού στερεού.
Στο δεύτερο σχήμα εμφανίζεται ένα τμήμα κυλινδρικης επιφάνειας  .
. (Συνέχεια...)
 είναι η έλλειψη:
είναι η έλλειψη: 




 είναι όγκος του χωρίου που περιβάλλεται από την κυλινδρική επιφάνεια με οδηγό την καμπύλη
είναι όγκος του χωρίου που περιβάλλεται από την κυλινδρική επιφάνεια με οδηγό την καμπύλη  ,
, και από ένα τμήμα του δίχωνου υπερβολοειδούς.
και από ένα τμήμα του δίχωνου υπερβολοειδούς. 
 είναι ο όγκος του χωρίου που περιβάλλεται από την ίδια κυλινδρική επιφάνεια που αναφέρθηκε προηγούμενα,
είναι ο όγκος του χωρίου που περιβάλλεται από την ίδια κυλινδρική επιφάνεια που αναφέρθηκε προηγούμενα,  και από την επιφάνεια του μονόχωνου υπερβολοειδούς.
και από την επιφάνεια του μονόχωνου υπερβολοειδούς. 
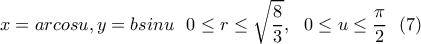

(Συνέχεια...)


 και
και 





 αλλά με τους περιορισμούς:
αλλά με τους περιορισμούς:  και
και 
 παραμένουν ίδιες και συνεπώς θα είναι:
παραμένουν ίδιες και συνεπώς θα είναι: 

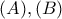 θα είναι:
θα είναι: 
 θα είναι:
θα είναι: 
 είναι οι αριθμητικοί συντελεστές των τύπων
είναι οι αριθμητικοί συντελεστές των τύπων 
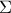 το στερεό που περικλείεται από το μονόχωνο υπερβολοειδές
το στερεό που περικλείεται από το μονόχωνο υπερβολοειδές  και το δίχωνο υπερβολοειδές
και το δίχωνο υπερβολοειδές  .
.  και λύνοντας το σύστημα
και λύνοντας το σύστημα
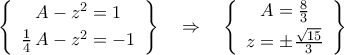
 Μια παραμετρική παράσταση της επιφάνειας
Μια παραμετρική παράσταση της επιφάνειας  είναι
είναι ![\displaystyle{\overline{R}(u,v)=\big(\alpha\cosh{u}\,\cos({-v}),\beta\cosh{u}\,\sin({-v}),\sinh{u}\big)\,,\quad (u,v)\in\big[-\sinh^{-1}\big(\tfrac{\sqrt{15}}{3}\big),\sinh^{-1}\big(\tfrac{\sqrt{15}}{3}\big)\big]\times[0,2\pi]\,,} \displaystyle{\overline{R}(u,v)=\big(\alpha\cosh{u}\,\cos({-v}),\beta\cosh{u}\,\sin({-v}),\sinh{u}\big)\,,\quad (u,v)\in\big[-\sinh^{-1}\big(\tfrac{\sqrt{15}}{3}\big),\sinh^{-1}\big(\tfrac{\sqrt{15}}{3}\big)\big]\times[0,2\pi]\,,}](/forum/ext/geomar/texintegr/latexrender/pictures/afc4038fb1e44c51bbf77b493f1d1dde.png)
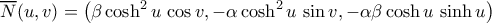 , το οποίο "δείχνει" προς το εξωτερικό του στερεού
, το οποίο "δείχνει" προς το εξωτερικό του στερεού 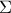 . Ομοίως μια παραμετρική παράσταση του "θετικού" τμήματος
. Ομοίως μια παραμετρική παράσταση του "θετικού" τμήματος  της επιφάνειας
της επιφάνειας  είναι
είναι ![\displaystyle{\overline{R}_1(u,v)=\big(2\alpha\sinh{u}\,\cos{v},2\beta\sinh{u}\,\sin{v},\cosh{u}\big)\,,\quad (u,v)\in\big[0,\cosh^{-1}\big(\tfrac{\sqrt{15}}{3}\big)\big]\times[0,2\pi]\,,} \displaystyle{\overline{R}_1(u,v)=\big(2\alpha\sinh{u}\,\cos{v},2\beta\sinh{u}\,\sin{v},\cosh{u}\big)\,,\quad (u,v)\in\big[0,\cosh^{-1}\big(\tfrac{\sqrt{15}}{3}\big)\big]\times[0,2\pi]\,,}](/forum/ext/geomar/texintegr/latexrender/pictures/9c8bbfbbb911bd61e4069e066119da5e.png)
 το οποίο "δείχνει" προς το εξωτερικό του στερεού
το οποίο "δείχνει" προς το εξωτερικό του στερεού 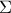 , ενώ μια παραμετρική παράσταση του "αρνητικού" τμήματος
, ενώ μια παραμετρική παράσταση του "αρνητικού" τμήματος 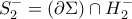 της επιφάνειας
της επιφάνειας  είναι
είναι ![\displaystyle{\overline{R}_2(u,v)=\big(2\alpha\sinh{u}\,\cos({-v}),2\beta\sinh{u}\,\sin({-v}),-\cosh{u}\big)\,,\quad (u,v)\in\big[0,\cosh^{-1}\big(\tfrac{\sqrt{15}}{3}\big)\big]\times[0,2\pi]\,,} \displaystyle{\overline{R}_2(u,v)=\big(2\alpha\sinh{u}\,\cos({-v}),2\beta\sinh{u}\,\sin({-v}),-\cosh{u}\big)\,,\quad (u,v)\in\big[0,\cosh^{-1}\big(\tfrac{\sqrt{15}}{3}\big)\big]\times[0,2\pi]\,,}](/forum/ext/geomar/texintegr/latexrender/pictures/1714abf1f36cd86019896c2bd54168a4.png)
 το οποίο "δείχνει" προς το εξωτερικό του στερεού
το οποίο "δείχνει" προς το εξωτερικό του στερεού 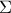 .
. , από το θεώρημα απόκλισης προκύπτει ότι
, από το θεώρημα απόκλισης προκύπτει ότι 

Δίνουμε και σε αυτό το ερώτημα μια λύση:
 , (με τον προσανατολισμό που επιλέχθηκε παραπάνω) μια παραμετρική παράσταση του θετικά προσανατολισμένου συνόρου της
, (με τον προσανατολισμό που επιλέχθηκε παραπάνω) μια παραμετρική παράσταση του θετικά προσανατολισμένου συνόρου της  είναι
είναι ![\overline{c}(t)=\begin{cases}
\Big(\tfrac{2\alpha\sqrt{2}}{\sqrt{3}}\cos({-t}),\tfrac{2\beta\sqrt{2}}{\sqrt{3}}\sin({-t}),\tfrac{\sqrt{15}}{3}\Big)\,,& t\in[0,2\pi]\\\noalign{\vspace{0.2cm}}
\Big(\tfrac{2\alpha\sqrt{2}}{\sqrt{3}}\cos{t},\tfrac{2\beta\sqrt{2}}{\sqrt{3}}\sin{t},-\tfrac{\sqrt{15}}{3}\Big)\,,& t\in[2\pi,4\pi]
\end{cases}\,. \overline{c}(t)=\begin{cases}
\Big(\tfrac{2\alpha\sqrt{2}}{\sqrt{3}}\cos({-t}),\tfrac{2\beta\sqrt{2}}{\sqrt{3}}\sin({-t}),\tfrac{\sqrt{15}}{3}\Big)\,,& t\in[0,2\pi]\\\noalign{\vspace{0.2cm}}
\Big(\tfrac{2\alpha\sqrt{2}}{\sqrt{3}}\cos{t},\tfrac{2\beta\sqrt{2}}{\sqrt{3}}\sin{t},-\tfrac{\sqrt{15}}{3}\Big)\,,& t\in[2\pi,4\pi]
\end{cases}\,.](/forum/ext/geomar/texintegr/latexrender/pictures/a5c50b2e54b9ba4b11b7f9e43fecf5c1.png)


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες