Θα αρχίσω από το (2). Ο ορισμός του

είναι

όπου το

είναι μοναδιαίο διάνυσμα κάθετο στην επιφάνεια. Υπάρχουν δύο επιλογές για το

γι' αυτό πρέπει να δίνεται ο προσανατολισμός.
Για το (1) τώρα, η παραμετροποίηση που έγραψες είναι σωστή και πρέπει να δουλέψει. Πρόσεξε επίσης τα εξής
(α) Να βάλεις τα όρια σωστά. Τόσο το

όσο και το
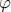
πρέπει να κινούνται από

ως

.
(β) Δεν πρέπει να ξεχάσεις ότι το

γίνεται

. Κοίταξε ξανά τις σημειώσεις σου να βεβαιωθείς γιατί ισχύει αυτό και πώς να βρίσκεις το

για άλλες επιφάνειες.
Είναι σημαντικό να επιλέγουμε την απλούστερη παραμετροποίηση και για αυτό το παράδειγμα είναι η πιο πάνω. Θα μπορούσαμε επίσης να επιλέξουμε την παραμετροποίηση

. Εδώ υπάρχει και η δυσκολία να βρούμε ποια είναι τα όρια. Αν π.χ. ολοκληρώσαμε πρώτα ως προς

και μετά ως προς

, τότε τα όρια του

θα εξαρτιώνται από το

. (Δοκίμασε να τα βρεις.) Μετά τα όρια του

είναι εύκολα. Απλά πάμε από το

ως το

. Δοκίμασε και με αυτόν τον τρόπο να δεις αν βγάζεις την ίδια απάντηση.
Πιθανώς να έχεις ήδη δει και κάποια θεωρήματα τα οποία συχνά μας βοηθάνε. Π.χ. εδώ θα μπορούσαμε να χρησιμοποιήσουμε και το Θεώρημα Αποκλίσεως (Divergence Theorem) αλλά όχι απευθείας επειδή η επιφάνειά μας δεν είναι κλειστή.
 όπου
όπου  και το
και το  είναι το κομμάτι της μοναδιαίας σφαίρας του στο πρώτο ογδοοκύκλιο με εξωτερικό προσανατολισμό.
είναι το κομμάτι της μοναδιαίας σφαίρας του στο πρώτο ογδοοκύκλιο με εξωτερικό προσανατολισμό. και τα νούμερα δεν βγήκαν όπως θα έπρεπε.
και τα νούμερα δεν βγήκαν όπως θα έπρεπε.
 είναι
είναι  όπου το
όπου το  είναι μοναδιαίο διάνυσμα κάθετο στην επιφάνεια. Υπάρχουν δύο επιλογές για το
είναι μοναδιαίο διάνυσμα κάθετο στην επιφάνεια. Υπάρχουν δύο επιλογές για το  όσο και το
όσο και το 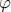 πρέπει να κινούνται από
πρέπει να κινούνται από  ως
ως  .
. γίνεται
γίνεται  . Κοίταξε ξανά τις σημειώσεις σου να βεβαιωθείς γιατί ισχύει αυτό και πώς να βρίσκεις το
. Κοίταξε ξανά τις σημειώσεις σου να βεβαιωθείς γιατί ισχύει αυτό και πώς να βρίσκεις το  . Εδώ υπάρχει και η δυσκολία να βρούμε ποια είναι τα όρια. Αν π.χ. ολοκληρώσαμε πρώτα ως προς
. Εδώ υπάρχει και η δυσκολία να βρούμε ποια είναι τα όρια. Αν π.χ. ολοκληρώσαμε πρώτα ως προς  και μετά ως προς
και μετά ως προς  , τότε τα όρια του
, τότε τα όρια του  . Δοκίμασε και με αυτόν τον τρόπο να δεις αν βγάζεις την ίδια απάντηση.
. Δοκίμασε και με αυτόν τον τρόπο να δεις αν βγάζεις την ίδια απάντηση.
 ,
,  και
και 

 .
. . Κι αυτό έχει σημασία!
. Κι αυτό έχει σημασία!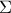 της σφαίρας
της σφαίρας  για
για  είναι
είναι ![\displaystyle {\overline{R}}(\varphi, \vartheta)=\big(\cos\varphi\sin\vartheta,\,\sin\varphi\sin\vartheta,\,\cos\vartheta\big)\,,\;\varphi\in\big[0,\tfrac{\pi}{2}\big], \; \vartheta\in\big[0,\tfrac{\pi}{2}\big]\,. \displaystyle {\overline{R}}(\varphi, \vartheta)=\big(\cos\varphi\sin\vartheta,\,\sin\varphi\sin\vartheta,\,\cos\vartheta\big)\,,\;\varphi\in\big[0,\tfrac{\pi}{2}\big], \; \vartheta\in\big[0,\tfrac{\pi}{2}\big]\,.](/forum/ext/geomar/texintegr/latexrender/pictures/c03c51aa08e934a1ab38503da6de71e5.png)
![\varphi\in\big[0,\tfrac{\pi}{2}\big], \; \vartheta\in\big(0,\tfrac{\pi}{2}\big] \varphi\in\big[0,\tfrac{\pi}{2}\big], \; \vartheta\in\big(0,\tfrac{\pi}{2}\big]](/forum/ext/geomar/texintegr/latexrender/pictures/b9adc3dd0cbfbf50136e9e21f8af6904.png) , ισχύει
, ισχύει  . Παρότι
. Παρότι 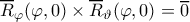 θεωρώντας σαν (θετικά προσανατολισμένο) μοναδιαίο κάθετο στην
θεωρώντας σαν (θετικά προσανατολισμένο) μοναδιαίο κάθετο στην  μπορούμε να προχωρήσουμε στον υπολογισμό
μπορούμε να προχωρήσουμε στον υπολογισμό 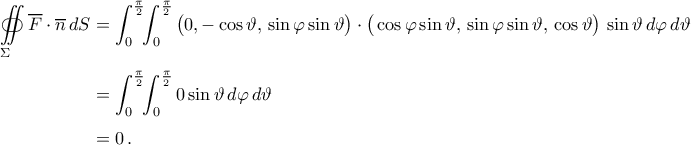
 επεκτείνεται σε μια συνεχώς διαφορίσιμη συνάρτηση
επεκτείνεται σε μια συνεχώς διαφορίσιμη συνάρτηση  , όπου
, όπου  ένα ανοικτό σύνολο με
ένα ανοικτό σύνολο με ![\big[0,\tfrac{\pi}{2}\big]\times\big[0,\tfrac{\pi}{2}\big]\subset U \big[0,\tfrac{\pi}{2}\big]\times\big[0,\tfrac{\pi}{2}\big]\subset U](/forum/ext/geomar/texintegr/latexrender/pictures/053a48fcc067738031adc33f75f83b66.png) .
. το στερεό που είναι το κομμάτι της σφαίρας μαζί με τα επίπεδα που το καθορίζουν.
το στερεό που είναι το κομμάτι της σφαίρας μαζί με τα επίπεδα που το καθορίζουν. (1)
(1)








