Σελίδα 1 από 1
Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Τετ Φεβ 12, 2020 4:25 pm
από Maidenas
Να υπολογιστεί το μήκος της καμπήλης

όπου

To ολοκλήρωμα που θα προκύψει το έχω ήδη λύσει με 2 διαφορετικούς τρόπους και αυτος ειναι ο 3ος. Για να επαληθεύσω τα αποτελέσατα έθεσα στο τέλος όπου

και βρίσκω οτι το μήκος της καμπύλης ειναι περίπου ίσο με

Παρόλα αυτά με τον τρίτο τρόπο δεν παίρνω το αποτέλεσμα που θέλω, και παρόλο που το έχω ελέγξει απειρες φορές δεν βρίσκω άκρη.
Έχουμε

θετω

και
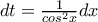
Οπότε όταν

και

Οπότε το ολοκλήρωμα με την αντικατάσταση αυτή θα γίνει:

Εφαρμόζω παραγοντική ολοκλήρωση εδώ, άρα
![\int_{0}^{tan^{-1}(a)}(tanx)' \frac{1}{cosx}dx= \left [tanx \frac{1}{cosx} \right ]_{x=0}^{tan^{-1}(a)}- \int_{0}^{tan^{-1}(a)} \frac{sinx}{cosx} \frac{sinx}{cos^2x}dx \int_{0}^{tan^{-1}(a)}(tanx)' \frac{1}{cosx}dx= \left [tanx \frac{1}{cosx} \right ]_{x=0}^{tan^{-1}(a)}- \int_{0}^{tan^{-1}(a)} \frac{sinx}{cosx} \frac{sinx}{cos^2x}dx](/forum/ext/geomar/texintegr/latexrender/pictures/92f7d82e751a67f366296ca591a2b406.png)



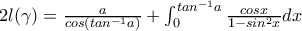
Νέα αντικατάσταση όπου



Οπότε παίρνουμε:


![2 l(\gamma)=\frac{a}{cos(tan^{-1}a)} + \frac{1}{2} \left [ ln|1-t| \right ]_0 ^{sin(tan^{-1}a)} + \frac{1}{2} \left [ ln|1+t| \right ]_0 ^{sin(tan^{-1}a)} 2 l(\gamma)=\frac{a}{cos(tan^{-1}a)} + \frac{1}{2} \left [ ln|1-t| \right ]_0 ^{sin(tan^{-1}a)} + \frac{1}{2} \left [ ln|1+t| \right ]_0 ^{sin(tan^{-1}a)}](/forum/ext/geomar/texintegr/latexrender/pictures/d0194bb49645bddc06367d66ddcb18a6.png)
![l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) + \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ] l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) + \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/c93c5c89190717cc43279a55bdbd86fb.png)
Αν βάλω όπου α=1 δεν παίρνω το αποτέλεσμα που θέλω...
Πειραματίστηκα λίγο με τα πρόσημα και πρόσεξα οτι στο τέλος αν είχα αυτό
![l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) - \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ] l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) - \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/36e08f4ffd151e60a073458491a72c85.png)
τότε για α=1 παίρνω το ζητούμενο αποτέλεσμα.
Ωστοσο επειδη το έλεγξα αυτό το σημείο, δεν γίνεται να βγει εκεί με μείον.
Μπορεί κανείς να με βοηθήσει;;
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Τετ Φεβ 12, 2020 7:37 pm
από Mihalis_Lambrou
Δεν το κοίταξα με λεπτομέρεια γιατί χάνεσαι χωρίς λόγο. Πολλές πράξεις χωρίς αιτία.
Το ολοκλήρωμα που ψάχνεις μετά την αντικατάσταση είναι το

που είναι στάνταρ και υπάρχει σε όλα τα βιβλία που έχουν καλή διαπραγμάτευση τεχνικών ολοκλήρωσης. Ίσον, σχεδόν όλοι οι Απειροστικοί Λογισμοί και οι Αναλύσεις.
Με την σειρά του αυτό ανάγεται στο

.
Υπόδειξη για το τελευταίο: Ίσως ο γρηγορότερος τρόπος είναι με

.
Άλλος στάνταρ τρόπος είναι με την αλλαγή μεταβλητής

.
Με λίγα λόγια, βρες πρώτα το αόριστο ολοκλήρωμα και μετά βάλε τα όρια. Θα γλυτώσεις έτσι παραστάσεις όπως

που κουβαλάς μέχρι εξαντλήσεως.
Περιμένουμε εδώ τις λύσεις σου.
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Τετ Φεβ 12, 2020 11:11 pm
από Maidenas
Mihalis_Lambrou έγραψε: ↑Τετ Φεβ 12, 2020 7:37 pm
Το ολοκλήρωμα που ψάχνεις μετά την αντικατάσταση είναι το

που είναι στάνταρ και υπάρχει σε όλα τα βιβλία που έχουν καλή διαπραγμάτευση τεχνικών ολοκλήρωσης. Ίσον, σχεδόν όλοι οι Απειροστικοί Λογισμοί και οι Αναλύσεις.
Μπορεί να σας εκπλήξω, αλλά ποτέ σε κανένα μάθημα στο Μαθηματικό αθήνας δεν το έχουμε συναντήσει το secx. (εννοώ σε κανέναν απο τους τρεις απειροστικούς και διαφορική γεωμετρία) Δεν είναι τίποτα άλλο βέβαια απο
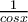
Οπότε ειναι λίγο θέμα εξοικίωσης.
Αν στη δική μου λύση πάω να λύσω το αόριστο ολοκλήρωμα και βάλω όπου
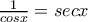
τότε στο σημείο

δεν θα μας είναι πρόβλημα το απόλυτο;
Ενω με το ορισμένο ολοκλήρωμα επειδή δίνεται οτι

άρα το

τότε μπορώ να συμπεράνω οτι

και να αφαιρέσω το απόλυτο.
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Τετ Φεβ 12, 2020 11:31 pm
από Maidenas
Οι αλλοι 2 τρόποι που προσπάθησα ήταν:
Ο 1ος: έθεσα

και ο 2ος:

(o 2ος ήταν και ο πιο σύντομος)
Απλά με προβλημάτισε πολύ που δεν έβγαλα το ίδιο αποτέλεσμα με τον τρίτο τρόπο και δεν κατάλαβα που έκανα το λάθος.
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 8:25 am
από Mihalis_Lambrou
Maidenas έγραψε: ↑Τετ Φεβ 12, 2020 11:11 pm
Μπορεί να σας εκπλήξω, αλλά ποτέ σε κανένα μάθημα στο Μαθηματικό αθήνας δεν το έχουμε συναντήσει το secx. (εννοώ σε κανέναν απο τους τρεις απειροστικούς και διαφορική γεωμετρία) Δεν είναι τίποτα άλλο βέβαια απο
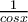
Οπότε ειναι λίγο θέμα εξοικίωσης.
Μάλλον δεν τα λες καλά.
Βλέπε π.χ. Νεγρεπόντης et al, τόμος ΙΙ1 σελίς 254 (το

) και αλλού,
Spivak, σελίδες 329, 336, 348, 349 και αλλού. Και λοιπά, και λοιπά.
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 1:58 pm
από Maidenas
Mihalis_Lambrou έγραψε: ↑Πέμ Φεβ 13, 2020 8:25 am
Μάλλον δεν τα λες καλά.
Βλέπε π.χ. Νεγρεπόντης et al, τόμος ΙΙ1 σελίς 254 (το

) και αλλού,
Spivak, σελίδες 329, 336, 348, 349 και αλλού. Και λοιπά, και λοιπά.
Για τους απειροστικούς Ι και ΙΙ προτείνεται οι σημειώσεις του κυρίου Γιαννόπουλου που ειναι υπερπλήρεις, αλλά το secχ δεν το χρησιμοποιήσαμε ποτέ, θα μπορούσε να σας το επιβεβαίωσει οποιοσδήποτε φοιτητής του μαθηματικού Αθηνών. Στην ουσία είναι ο συμβολισμός του
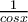
που το μονο που χρειάζεται ειναι εξοικίωση. Δεν μπήκαμε ποτέ σε αυτή την διαδικασία γιατί δεν μας το ανέφεραν.
Συγκεκριμένα για το σύγγραμα του κυρίου Νεγρεπόντη μας λέγαν το εξής: Οτι είναι εξαιρετικό σύγγραμμα, πολύ αυστηρό, απλώς για τους πρωτοετείς θα φαινόταν κάπως, οπότε δεν μας το συνιστούσαν ιδιαίτερα. Κάποια στιγμή θα το βρίσκαμε μπροστά μας βέβαια.
Τελικά για το ολοκλήρωμα εντόπισα το λάθος που χει γίνει. Στην αντιπαράγωγο του

. Οπότε βγαίνει σωστά έτσι με αυτήν την διόρθωση.
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 8:55 pm
από Mihalis_Lambrou
Maidenas έγραψε: ↑Πέμ Φεβ 13, 2020 1:58 pm
θα μπορούσε να σας το επιβεβαίωσει
οποιοσδήποτε φοιτητής του μαθηματικού Αθηνών. .
Πάλι δεν τα λες καλά. Με το σύστημα "Εύδοξος" πολλαπλού βιβλίου, ο κάθε φοιτητής επιλέγει από μία λίστα εκείνο το βιβλίο που του αρέσει. Στον "Εύδοξο" υπάρχει και το βιβλίο του Νεγρεπόντη και του Spivak, οπότε δεν μπορείς να ξέρεις τι πήραν οι συμφοιτητές σου, τους οποίους επικαλείσαι.
Αλλά δεν είναι εκεί το θέμα. Το σημαντικότερο είναι ότι αλίμονο αν μένουμε σε ένα βιβλίο. Εξαιρετικό μεν, όπως και τα άλλα δύο, αλλά αν όλες μας οι γνώσεις περικλείονται ανάμεσα σε δύο εξώφυλλα και μόνο, βαδίζουμε σε λάθος μονοπάτι.
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 9:49 pm
από Tolaso J Kos
Χωρίς να θέλω να παρέμβω στη κουβέντα , αλλά , μία ωραία τεχνική για αυτού του είδους τα ολοκληρώματα είναι οι παράγοντες. Για παράδειγμα:

και τα λοιπά.
Αποφεύγουμε τη τριγωνομετρική αντικατάσταση και τα ακόλουθα της. Βεβαία η αντικατάσταση  είναι βολική !!
είναι βολική !!
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 10:27 pm
από Maidenas
Mihalis_Lambrou έγραψε: ↑Πέμ Φεβ 13, 2020 8:55 pm
Πάλι δεν τα λες καλά. Με το σύστημα "Εύδοξος" πολλαπλού βιβλίου, ο κάθε φοιτητής επιλέγει από μία λίστα εκείνο το βιβλίο που του αρέσει. Στον "Εύδοξο" υπάρχει και το βιβλίο του Νεγρεπόντη και του Spivak, οπότε δεν μπορείς να ξέρεις τι πήραν οι συμφοιτητές σου, τους οποίους επικαλείσαι.
Αλλά δεν είναι εκεί το θέμα. Το σημαντικότερο είναι ότι αλίμονο αν μένουμε σε ένα βιβλίο. Εξαιρετικό μεν, όπως και τα άλλα δύο, αλλά αν όλες μας οι γνώσεις περικλείονται ανάμεσα σε δύο εξώφυλλα και μόνο, βαδίζουμε σε λάθος μονοπάτι.
Δεν αντιλέγω σε αυτό. Συγκεκριμένα εγώ μάλιστα έχω και του Spivak το βιβλίο, και του κύριου Νεγρεπόντη. Απλώς για κάποιο λόγο δεν έχουμε δει ποτέ απο καθηγητες στους απειροστικούς να χρησιμοποιούν στον πίνακα το secx στην θέση του
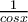
.
Πάντως και να θέλαμε να μείνουμε σε ένα βιβλίο δεν γίνεται εκ των πραγμάτων, είναι τόσο απαιτητική η σχολή, που αμα δεν ψάξουμε συγχρόνως σημειώσεις απο την τάξη, ιντερνετ, και οποιοδήποτε βιβλίο έχουμε δεν γίνεται αλλιώς.
Ας πούμε στην Μιγαδική ανάλυση έβλεπα κάτι καταπληκτικά βιντεομαθήματα αυτής της εξαιρετικής καθηγήτριας.
https://www.youtube.com/playlist?list=P ... eH0RaBoYJf
Γραμμικες Άλγεβρες , απο Gilbert Strang του MIT, του χρωστάω το 9 που έγραψα Γραμμικη.
Απειροστικό 3 απο ένα εβραϊκό πανεπιστήμιο , απίθανος καθηγητής και αυτός:
https://www.youtube.com/watch?v=oV0INtZ ... Bp-fhWrDr0
Γενικά, ψαχνόμαστε πολύ!!
Και θα ήταν αμαρτία αμα δεν αναφέρω και την υπερπολύτιμη βοήθεια που έχω πάρει απο αυτό φόρουμ!!! Τυχαίνει να διαβάζω ασκήσεις που κατα καιρούς ανεβάζετε εδώ και εκπλήσσομαι με την ποικιλία των τρόπων που τις αποδεικνύεται...
Re: Ένα μικρούλι ολοκλήρωμα που γιγαντώνεται
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 10:29 pm
από Maidenas
Tolaso J Kos έγραψε: ↑Πέμ Φεβ 13, 2020 9:49 pm
Χωρίς να θέλω να παρέμβω στη κουβέντα , αλλά , μία ωραία τεχνική για αυτού του είδους τα ολοκληρώματα είναι οι παράγοντες. Για παράδειγμα:

και τα λοιπά.
Αποφεύγουμε τη τριγωνομετρική αντικατάσταση και τα ακόλουθα της. Βεβαία η αντικατάσταση  είναι βολική !!
είναι βολική !!
Πολύ καλός τρόπος!!! Ευχαριστώ πολύ

όπου
 και βρίσκω οτι το μήκος της καμπύλης ειναι περίπου ίσο με
και βρίσκω οτι το μήκος της καμπύλης ειναι περίπου ίσο με  Παρόλα αυτά με τον τρίτο τρόπο δεν παίρνω το αποτέλεσμα που θέλω, και παρόλο που το έχω ελέγξει απειρες φορές δεν βρίσκω άκρη.
Παρόλα αυτά με τον τρίτο τρόπο δεν παίρνω το αποτέλεσμα που θέλω, και παρόλο που το έχω ελέγξει απειρες φορές δεν βρίσκω άκρη.
 και
και 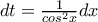



![\int_{0}^{tan^{-1}(a)}(tanx)' \frac{1}{cosx}dx= \left [tanx \frac{1}{cosx} \right ]_{x=0}^{tan^{-1}(a)}- \int_{0}^{tan^{-1}(a)} \frac{sinx}{cosx} \frac{sinx}{cos^2x}dx \int_{0}^{tan^{-1}(a)}(tanx)' \frac{1}{cosx}dx= \left [tanx \frac{1}{cosx} \right ]_{x=0}^{tan^{-1}(a)}- \int_{0}^{tan^{-1}(a)} \frac{sinx}{cosx} \frac{sinx}{cos^2x}dx](/forum/ext/geomar/texintegr/latexrender/pictures/92f7d82e751a67f366296ca591a2b406.png)



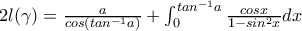





![2 l(\gamma)=\frac{a}{cos(tan^{-1}a)} + \frac{1}{2} \left [ ln|1-t| \right ]_0 ^{sin(tan^{-1}a)} + \frac{1}{2} \left [ ln|1+t| \right ]_0 ^{sin(tan^{-1}a)} 2 l(\gamma)=\frac{a}{cos(tan^{-1}a)} + \frac{1}{2} \left [ ln|1-t| \right ]_0 ^{sin(tan^{-1}a)} + \frac{1}{2} \left [ ln|1+t| \right ]_0 ^{sin(tan^{-1}a)}](/forum/ext/geomar/texintegr/latexrender/pictures/d0194bb49645bddc06367d66ddcb18a6.png)
![l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) + \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ] l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) + \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/c93c5c89190717cc43279a55bdbd86fb.png)
![l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) - \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ] l(\gamma)= \frac{1}{2}\left [ \frac{a}{cos(tan^{-1}a)} + \frac{1}{2} ln(1+sin(tan^{-1}a)) - \frac{1}{2} ln( 1 - sin(tan^{-1}a)) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/36e08f4ffd151e60a073458491a72c85.png)

 που είναι στάνταρ και υπάρχει σε όλα τα βιβλία που έχουν καλή διαπραγμάτευση τεχνικών ολοκλήρωσης. Ίσον, σχεδόν όλοι οι Απειροστικοί Λογισμοί και οι Αναλύσεις.
που είναι στάνταρ και υπάρχει σε όλα τα βιβλία που έχουν καλή διαπραγμάτευση τεχνικών ολοκλήρωσης. Ίσον, σχεδόν όλοι οι Απειροστικοί Λογισμοί και οι Αναλύσεις.  .
.  .
. .
. που κουβαλάς μέχρι εξαντλήσεως.
που κουβαλάς μέχρι εξαντλήσεως.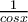 Οπότε ειναι λίγο θέμα εξοικίωσης.
Οπότε ειναι λίγο θέμα εξοικίωσης.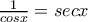 τότε στο σημείο
τότε στο σημείο  δεν θα μας είναι πρόβλημα το απόλυτο;
δεν θα μας είναι πρόβλημα το απόλυτο; άρα το
άρα το  τότε μπορώ να συμπεράνω οτι
τότε μπορώ να συμπεράνω οτι  και να αφαιρέσω το απόλυτο.
και να αφαιρέσω το απόλυτο.
 (o 2ος ήταν και ο πιο σύντομος)
(o 2ος ήταν και ο πιο σύντομος) ) και αλλού,
) και αλλού, . Οπότε βγαίνει σωστά έτσι με αυτήν την διόρθωση.
. Οπότε βγαίνει σωστά έτσι με αυτήν την διόρθωση.
 είναι βολική !!
είναι βολική !!