Άθροισμα Riemann: Συλλογή ασκήσεων
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
- Tolaso J Kos
- Δημοσιεύσεις: 5225
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Άσκηση 17
Να υπολογιστεί το όριο:

Να υπολογιστεί το όριο:

Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Είναι ουσιαστικά ίδια με την άσκηση 2 (πλην δευτερεύουσας αλλαγής στα νούμερα). Είναι λυμένη στο ποστ #5 και δεύτερη λύση στο ποστ #7.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Θα χρησιμοποιήσω ομοιόμορφη συνέχεια αλλά ως όφελος δεν θα χρησιμοποιήσω την υπόθεση ότι ηMihalis_Lambrou έγραψε: ↑Σάβ Ιαν 11, 2020 10:09 amΈχω παρατηρήσει ότι μερικές από τις παραπάνω ασκήσεις εμπίπτουν στην εξής περίπτωση, την οποία θέτω ως άσκηση
Άσκηση 13
Έστωσυνεχής και μονότονη συνάρτηση και έστω
ακολουθία θετικών όρων με
. Τότε
(Ωραίο θέμα για διαγώνισμα. Γιατί δεν το είχα σκεφθεί παλαιότερα...)
(Η μονοτονία δεν χρειάζεται. Απλά κάνει την ζωή ευκολότερη αλλά η άσκηση είναι προσιτή έτσι και αλλιώς. Η μονοτονία χρησιμοποιεί λιγότερα εργαλεία).
 είναι μονότονη. Αν χρησιμοποιήσουμε την μονοτονία η άσκηση γίνεται ευκολότερη και λύνεται χωρίς χρήση της ομοιόμορφης συνέχειας.
είναι μονότονη. Αν χρησιμοποιήσουμε την μονοτονία η άσκηση γίνεται ευκολότερη και λύνεται χωρίς χρήση της ομοιόμορφης συνέχειας. Έστω
 . Από ομοιόμορφη συνέχεια υπάρχει
. Από ομοιόμορφη συνέχεια υπάρχει  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε  με
με  είναι
είναι  .
. Έστω τώρα
 τέτοιο ώστε για
τέτοιο ώστε για  είναι
είναι  . Για τέτοια
. Για τέτοια  έχουμε
έχουμε  . Αθροίζοντας είναι
. Αθροίζοντας είναι  .
.Δεδομένου τώρα ότι
 , εύκολα καταλήγουμε ότο το όριο
, εύκολα καταλήγουμε ότο το όριο υπάρχει και ότι ισούμε με
υπάρχει και ότι ισούμε με 
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Μπορούμε να την κάνουμε απευθείας αλλά θα την κάνω με χρήση του έτοιμου αποτελέσματος της Άσκησης 9. ΈχουμεMihalis_Lambrou έγραψε: ↑Σάβ Ιαν 11, 2020 11:26 pmΆσκηση 14
Να υπολογισθεί το όριο της ακολουθίας
, όπου
.
(Πρόκειται για δίδυμο αδελφάκι της Άσκησης. Η ομοιότητα εκτός από οπτική, είναι βαθύτερη).
![\displaystyle{ \dfrac {1}{n} \sqrt [n] {\left(n+ d \right ) \left (n+ 2d \right ) \left (n+ 3d \right )\cdot ... \, \cdot \left (n+ nd)} \right )}} \displaystyle{ \dfrac {1}{n} \sqrt [n] {\left(n+ d \right ) \left (n+ 2d \right ) \left (n+ 3d \right )\cdot ... \, \cdot \left (n+ nd)} \right )}}](/forum/ext/geomar/texintegr/latexrender/pictures/abfb9d29380d73033d11f42f745d228b.png)
![\displaystyle{ = \dfrac {1}{n} \sqrt [n] {d^n n^n\left(\dfrac {1}{d} + \dfrac {1}{n} \right ) \left (\dfrac {1}{d} + \dfrac {2}{n} \right ) \left (\dfrac {1}{d} + \dfrac {3}{n} \right )\cdot ... \, \cdot \left (\dfrac {1}{d} + \dfrac {n}{n} \right )}}} \displaystyle{ = \dfrac {1}{n} \sqrt [n] {d^n n^n\left(\dfrac {1}{d} + \dfrac {1}{n} \right ) \left (\dfrac {1}{d} + \dfrac {2}{n} \right ) \left (\dfrac {1}{d} + \dfrac {3}{n} \right )\cdot ... \, \cdot \left (\dfrac {1}{d} + \dfrac {n}{n} \right )}}}](/forum/ext/geomar/texintegr/latexrender/pictures/602f8a88db6730479ca8f9bd6fee7096.png)
Αλλά από την Άσκηση 9 ζητάμε το
το οποίο είναι ουσιαστικά το ίδιο με το ζητούμενο αλλά μεMihalis_Lambrou έγραψε: ↑Σάβ Δεκ 28, 2019 10:32 pmΆσκηση 9
Να υπολογισθεί το όριο της ακολουθίας
, όπου
.
 αντί
αντί  . Έχουμε όμως έτοιμη την απάντηση
. Έχουμε όμως έτοιμη την απάντηση οπότε το ζητούμενο ισούται με

-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Με χρήση τηςMihalis_Lambrou έγραψε: ↑Πέμ Ιαν 16, 2020 11:22 pmΆσκηση 16
Να βρεθεί το όριο της ακολουθίας
, όπου
και
πραγματικός.
(τοδηλώνει ακέραιο μέρος.)
![k^ad -1 \le [k^ad] < k^ad k^ad -1 \le [k^ad] < k^ad](/forum/ext/geomar/texintegr/latexrender/pictures/593abf3390c12d5691772bf81a05a3e8.png) και αθροίζοντας έχουμε
και αθροίζοντας έχουμε ![\displaystyle{\dfrac {d}{n} \sum _{k=1}^{n} \left (\dfrac {k}{n} \right ) ^a - \dfrac {n}{n^{a+1}}\le \sum _{k=1}^{n} \dfrac {[k^ad]}{n^{a+1}}\le \dfrac {d}{n} \sum _{k=1}^{n} \left (\dfrac {k}{n} \right ) ^a } \displaystyle{\dfrac {d}{n} \sum _{k=1}^{n} \left (\dfrac {k}{n} \right ) ^a - \dfrac {n}{n^{a+1}}\le \sum _{k=1}^{n} \dfrac {[k^ad]}{n^{a+1}}\le \dfrac {d}{n} \sum _{k=1}^{n} \left (\dfrac {k}{n} \right ) ^a }](/forum/ext/geomar/texintegr/latexrender/pictures/0ced9db3dfb380cf3a37452c5dd48db5.png)
Παίρνοντας όριο
 και επειδή τα δύο άκρα έχουν κοινό όριο
και επειδή τα δύο άκρα έχουν κοινό όριο  , έπεται ότι το ζητούμενο όριο είναι
, έπεται ότι το ζητούμενο όριο είναι  .
.- Tolaso J Kos
- Δημοσιεύσεις: 5225
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Δύο δύσκολες κατά τη γνώμη μου ....
Άσκηση 18
Έστω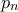 ο
ο  -οστός πρώτος και
-οστός πρώτος και  συνεχής συνάρτηση Riemann ολοκληρώσιμη στο
συνεχής συνάρτηση Riemann ολοκληρώσιμη στο  . Να δειχθεί ότι
. Να δειχθεί ότι

Άσκηση 19
Έστω συνεχής περιοδική συνάρτηση με περίοδο
συνεχής περιοδική συνάρτηση με περίοδο  και
και  ένας άρρητος αριθμός. Να δειχθεί ότι:
ένας άρρητος αριθμός. Να δειχθεί ότι:

Άσκηση 18
Έστω
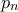 ο
ο  -οστός πρώτος και
-οστός πρώτος και  συνεχής συνάρτηση Riemann ολοκληρώσιμη στο
συνεχής συνάρτηση Riemann ολοκληρώσιμη στο  . Να δειχθεί ότι
. Να δειχθεί ότι 
Άσκηση 19
Έστω
 συνεχής περιοδική συνάρτηση με περίοδο
συνεχής περιοδική συνάρτηση με περίοδο  και
και  ένας άρρητος αριθμός. Να δειχθεί ότι:
ένας άρρητος αριθμός. Να δειχθεί ότι:
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5225
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Άθροισμα Riemann: Συλλογή ασκήσεων
Άσκηση 20
Να υπολογιστεί το όριο .
.
Να υπολογιστεί το όριο
 .
.Η φαντασία είναι σημαντικότερη από τη γνώση !


Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Ιάσων Κωνσταντόπουλος και 4 επισκέπτες

 και
και 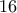 .
.

 όπου
όπου