Ολοκλήρωμα με Γ
Δημοσιεύτηκε: Παρ Δεκ 13, 2019 10:35 pm
Έστω  η συνάρτηση Γάμμα του Euler. Να δειχθεί ότι:
η συνάρτηση Γάμμα του Euler. Να δειχθεί ότι:
 όταν
όταν  .
.
 η συνάρτηση Γάμμα του Euler. Να δειχθεί ότι:
η συνάρτηση Γάμμα του Euler. Να δειχθεί ότι: όταν
όταν  .
. η συνάρτηση Γάμμα του Euler. Να δειχθεί ότι:
η συνάρτηση Γάμμα του Euler. Να δειχθεί ότι: όταν
όταν  .
.


 οποιαδήποτε κυκλική περιφέρεια. Τότε
οποιαδήποτε κυκλική περιφέρεια. Τότε  .
. είναι μερόμορφη στο
είναι μερόμορφη στο  και ο μοναδικός της πόλος είναι ο
και ο μοναδικός της πόλος είναι ο 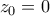 τάξης
τάξης  . Τότε,
. Τότε,
