![f:[0,1]\rightarrow [0,1] f:[0,1]\rightarrow [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/61de97806fe703f35371fc6edc830bb7.png)
η οποία είναι αύξουσα.
Υπάρχει
![c\in [0,1] c\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/6ea0a95f41192a6ad436a6874796e0cb.png)
με
 ;
;Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![f:\left[ 0,1 \right] \rightarrow \left[ 0,1 \right] f:\left[ 0,1 \right] \rightarrow \left[ 0,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/f5cd04e13df2f76764321f96c486b3e4.png) μια αύξουσα συνάρτηση τέτοια, ώστε
μια αύξουσα συνάρτηση τέτοια, ώστε 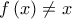 για κάθε
για κάθε ![x \in \left[ 0,1 \right] x \in \left[ 0,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0a81c54267b3ff9c569fc7d7d834daeb.png) . Θεωρούμε το σύνολο
. Θεωρούμε το σύνολο![A=\left\{ x\,\,\in \left[ 0,1 \right] \,\,: f\left( x \right) >x \right\}. A=\left\{ x\,\,\in \left[ 0,1 \right] \,\,: f\left( x \right) >x \right\}.](/forum/ext/geomar/texintegr/latexrender/pictures/a14a094feafeb11aa23225382f809d10.png)
 , γιατί από την υπόθεσή μας έχουμε ότι
, γιατί από την υπόθεσή μας έχουμε ότι  άρα
άρα  .
.![A\subseteq \left[ 0,1 \right] , A\subseteq \left[ 0,1 \right] ,](/forum/ext/geomar/texintegr/latexrender/pictures/15ce2dd6d8e1ba44312d4618dd0ab357.png) οπότε το
οπότε το  είναι άνω φραγμένο.
είναι άνω φραγμένο. 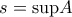 . Προφανώς, είναι
. Προφανώς, είναι ![s\in \left[ 0,1 \right] s\in \left[ 0,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0474c730f42071a87775b79558e4e02d.png) . Θα αποδείξουμε ότι
. Θα αποδείξουμε ότι  καταλήγοντας σε άτοπο και αποδεικνύοντας το ζητούμενο.
καταλήγοντας σε άτοπο και αποδεικνύοντας το ζητούμενο. Αν ήταν
Αν ήταν  τότε για κάθε
τότε για κάθε  θα είχαμε ότι
θα είχαμε ότι  , άρα
, άρα  , πράγμα άτοπο, αφού η
, πράγμα άτοπο, αφού η  είναι αύξουσα.
είναι αύξουσα. Αν ήταν
Αν ήταν  τότε θα υπήρχε
τότε θα υπήρχε  τέτοιο, ώστε
τέτοιο, ώστε  , άρα
, άρα  , πάλι άτοπο, αφού η
, πάλι άτοπο, αφού η  είναι αύξουσα.
είναι αύξουσα. οπότε το συμπέρασμα έπεται.
οπότε το συμπέρασμα έπεται. είναι φθίνουσα. Για παράδειγμα, η συνάρτηση
είναι φθίνουσα. Για παράδειγμα, η συνάρτηση 
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες