Σελίδα 1 από 1
Όριο αναδρομικής ακολουθίας
Δημοσιεύτηκε: Κυρ Σεπ 15, 2019 8:26 pm
από Tolaso J Kos
Ορίζουμε

και αναδρομικά

. Να υπολογιστεί το όριο:
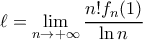
Re: Όριο αναδρομικής ακολουθίας
Δημοσιεύτηκε: Δευ Σεπ 16, 2019 6:04 pm
από sot arm
Tolaso J Kos έγραψε: ↑Κυρ Σεπ 15, 2019 8:26 pm
Ορίζουμε

και αναδρομικά

. Να υπολογιστεί το όριο:
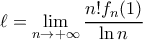
Μία λύση,παραλείπω κάποιες πράξεις ρουτίνας:
Επαγωγικά:

, οι μικρές περιπτώσεις είναι άμεσες και το επαγωγικό βήμα είναι μόνο μία παραγοντική.Άρα ψάχνουμε το:

Ο παρονομαστής είναι μη φραγμένη αύξουσα ακολουθία άρα από Cesaro-Stolz:

Re: Όριο αναδρομικής ακολουθίας
Δημοσιεύτηκε: Δευ Σεπ 16, 2019 8:18 pm
από Mihalis_Lambrou
sot arm έγραψε: ↑Δευ Σεπ 16, 2019 6:04 pm

Ο παρονομαστής είναι μη φραγμένη αύξουσα ακολουθία άρα από Cesaro-Stolz:

Ή, χάριν ποικιλίας, από την σταθερά Euler

έχουμε

Re: Όριο αναδρομικής ακολουθίας
Δημοσιεύτηκε: Δευ Σεπ 16, 2019 8:42 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
sot arm έγραψε: ↑Δευ Σεπ 16, 2019 6:04 pm
Tolaso J Kos έγραψε: ↑Κυρ Σεπ 15, 2019 8:26 pm
Ορίζουμε

και αναδρομικά

. Να υπολογιστεί το όριο:
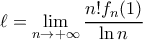
Μία λύση,παραλείπω κάποιες πράξεις ρουτίνας:
Επαγωγικά:

, οι μικρές περιπτώσεις είναι άμεσες και το επαγωγικό βήμα είναι μόνο μία παραγοντική.Άρα ψάχνουμε το:

Ο παρονομαστής είναι μη φραγμένη αύξουσα ακολουθία άρα από Cesaro-Stolz:

Γεια σου Σωτήρη.
Για Cesaro-Stolz εννοείς αυτό
https://en.wikipedia.org/wiki/Stolz%E2% ... ro_theorem
η κάτι άλλο;
Αν εννοείς το παραπάνω το έχεις εφαρμόσει ανάποδα.
Re: Όριο αναδρομικής ακολουθίας
Δημοσιεύτηκε: Δευ Σεπ 16, 2019 9:11 pm
από sot arm
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Σεπ 16, 2019 8:42 pm
sot arm έγραψε: ↑Δευ Σεπ 16, 2019 6:04 pm
Tolaso J Kos έγραψε: ↑Κυρ Σεπ 15, 2019 8:26 pm
Ορίζουμε

και αναδρομικά

. Να υπολογιστεί το όριο:
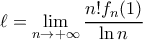
Μία λύση,παραλείπω κάποιες πράξεις ρουτίνας:
Επαγωγικά:

, οι μικρές περιπτώσεις είναι άμεσες και το επαγωγικό βήμα είναι μόνο μία παραγοντική.Άρα ψάχνουμε το:

Ο παρονομαστής είναι μη φραγμένη αύξουσα ακολουθία άρα από Cesaro-Stolz:

Γεια σου Σωτήρη.
Για Cesaro-Stolz εννοείς αυτό
https://en.wikipedia.org/wiki/Stolz%E2% ... ro_theorem
η κάτι άλλο;
Αν εννοείς το παραπάνω το έχεις εφαρμόσει ανάποδα.
Καλησπέρα, αυτό εννοώ. Σωστά, νομίζω, το έχω εφαρμόσει, απλα ίσως ο τροπος που το έγραψα να μην το κάνει ξεκάθαρο. Αφου το δευτερο όριο ισούται με - 1 και το ζητούμενο θα ισούται με

.
 και αναδρομικά
και αναδρομικά  . Να υπολογιστεί το όριο:
. Να υπολογιστεί το όριο: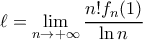
 και αναδρομικά
και αναδρομικά  . Να υπολογιστεί το όριο:
. Να υπολογιστεί το όριο: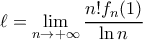
 και αναδρομικά
και αναδρομικά  . Να υπολογιστεί το όριο:
. Να υπολογιστεί το όριο: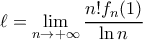
 , οι μικρές περιπτώσεις είναι άμεσες και το επαγωγικό βήμα είναι μόνο μία παραγοντική.Άρα ψάχνουμε το:
, οι μικρές περιπτώσεις είναι άμεσες και το επαγωγικό βήμα είναι μόνο μία παραγοντική.Άρα ψάχνουμε το:

 .
.