Παραγωγίσιμες και συνεχείς

Tolaso J Kos · #1

Έστω $\mathcal{F}$ η οικογένεια των παραγωγίσιμων συναρτήσεων $f:\mathbb{R} \rightarrow \mathbb{R}$ τέτοιες ώστε για κάθε ζευγάρι $x, y \in \mathbb{R}$ να ισχύει:

$\displaystyle{\frac{f(x)-f(y)}{x-y}=f'\left(\frac{x+y}{2}\right)}$
Δείξατε ότι κάθε συνάρτηση στο $\mathcal{F}$ είναι $\mathcal{C}^\infty$ .

Άνευ λύσης!

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #2

Tolaso J Kos έγραψε: ↑
Παρ Σεπ 13, 2019 7:52 am
Έστω $\mathcal{F}$ η οικογένεια των παραγωγίσιμων συναρτήσεων $f:\mathbb{R} \rightarrow \mathbb{R}$ τέτοιες ώστε για κάθε ζευγάρι $x, y \in \mathbb{R}$ να ισχύει:

$\displaystyle{\frac{f(x)-f(y)}{x-y}=f'\left(\frac{x+y}{2}\right)}$
Δείξατε ότι κάθε συνάρτηση στο $\mathcal{F}$ είναι $\mathcal{C}^\infty$ .

Άνευ λύσης!

Είναι γνωστή.
Κυκλοφορεί με το να βρεθούν όλες αυτές οι συναρτήσεις.
Δεν μαρτυράω ποιες είναι μήπως κάποιος θέλει να ασχοληθεί.
Σίγουρα έχει λυθεί στο

Μάλιστα θα είναι σε φάκελο Γ Λυκείου.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #3

Η αρχική διατύπωση είναι τελείως παραπλανητική.
Αφού δεν την βρίσκει κανείς γράφω μια λύση.
Να σημειώσω ότι την ξέρω από το 1975.Την έχω συναντήσει πολλές φορές κυρίως ως σχολική.

Για
$x+\frac{1}{2},x-\frac{1}{2}$
η σχέση γράφεται
$\displaystyle f(x+\frac{1}{2})-f(x-\frac{1}{2})=f'(x)$
Το αριστερό μέλος είναι παραγωγίσημη συνάρτηση .
Αρα είναι και το δεξί.
Αρα f''

υπάρχει.
Γράφοντας την σχέση ως $\displaystyle f(x)-f(y)=f'\left(\frac{x+y}{2}\right)}(x-y)$
παραγωγίζοντας πρώτα ως προς

για

σταθερό και μετά ανάποδα
παίρνουμε

$\displaystyle f'(x)=f''\left(\frac{x+y}{2}\right)}(x-y)\frac{1}{2}+f'\left(\frac{x+y}{2}\right)}$

$\displaystyle -f'(y)=f''\left(\frac{x+y}{2}\right)}(x-y)\frac{1}{2}-f'\left(\frac{x+y}{2}\right)}$

αφαιρόντας κατα μέλη προκύπτει

$\displaystyle f'(y)+f'(x)=2f'(\frac{x+y}{2})$

παραγωγίζοντας πρώτα ως προς

για

σταθερό και μετά ανάποδα την τελευταία
έχουμε
$\displaystyle f''(x)=f''(\frac{x+y}{2})=f''(y)$

Αρα f''

είναι σταθερή όποτε

$\displaystyle f(x)=ax^{2}+bx+c$

που προφανώς ικανοποιεί την συνθήκη.

#4

Διαφορετικά.

Έστω $t \neq 0$ . Τότε $\displaystyle f(x+2t) - f(x+t) = tf'\left( \tfrac{2x+3t}{2}\right)$ και $\displaystyle f(x+3t) - f(x) = 3tf'\left( \tfrac{2x+3t}{2}\right).$

Άρα $\displaystyle f(x+3t) - 3f(x+2t) + 3f(x+t) - f(x) = 0$ για κάθε

και κάθε $t \neq 0$ . Προφανώς ισχύει και για t=0

.

Ορίζουμε g(x) = f(x+t) - f(x)

και

και παίρνουμε διαδοχικά g(x+2t) - 2g(x+t) + g(x) = 0

και

. Αυτές ισχύουν για κάθε x,t

άρα η

είναι σταθερή και διαδοχικά η

είναι γραμμική και η

πολυώνυμική βαθμού το πολύ

.

Ας παρατηρήσουμε ότι και η εμφάνιση του

είναι παραπλανητική. Η ίδια απόδειξη δείχνει ότι αν $\displaystyle \frac{f(x)-f(y)}{x-y} = g(x+y)$ για κάποιες συναρτήσεις f,g

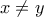και κάθε $x\neq y$ τότε η

είναι πολυώνυμική βαθμού το πολύ

.

Παραγωγίσιμες και συνεχείς

Παραγωγίσιμες και συνεχείς

Re: Παραγωγίσιμες και συνεχείς

Re: Παραγωγίσιμες και συνεχείς

Re: Παραγωγίσιμες και συνεχείς

Μέλη σε σύνδεση