https://www.mathematica.gr/forum/viewto ... =9&t=64775
Εστω
![f:[a,b]\rightarrow \mathbb{R} f:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/500b7d3e9c002fe33ef774ed310f6e88.png)
συνεχής συνάρτηση.
Εστω
![A\subseteq [a,b] A\subseteq [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/1ebff311d3b87fca4e7a1256d964f352.png) αριθμήσιμο σύνολο.
αριθμήσιμο σύνολο.Αν για κάθε
![x\in [a,b]-A x\in [a,b]-A](/forum/ext/geomar/texintegr/latexrender/pictures/42b89c0a2343abf13def40b114a47561.png)
είναι

να δειχθεί ότι η
 είναι σταθερή.
είναι σταθερή.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![f:[a,b]\rightarrow \mathbb{R} f:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/500b7d3e9c002fe33ef774ed310f6e88.png)
![A\subseteq [a,b] A\subseteq [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/1ebff311d3b87fca4e7a1256d964f352.png) αριθμήσιμο σύνολο.
αριθμήσιμο σύνολο.![x\in [a,b]-A x\in [a,b]-A](/forum/ext/geomar/texintegr/latexrender/pictures/42b89c0a2343abf13def40b114a47561.png)

 είναι σταθερή.
είναι σταθερή. . Θὰ δείξομε ὅτι
. Θὰ δείξομε ὅτι ![\displaystyle{
\max_{x\in[0,1]}f(x)-\min_{x\in[0,1]}f(x)<2\varepsilon,
} \displaystyle{
\max_{x\in[0,1]}f(x)-\min_{x\in[0,1]}f(x)<2\varepsilon,
}](/forum/ext/geomar/texintegr/latexrender/pictures/72fdebddebdbd45c69379ebd8e995dfb.png)
 σταθερά.
σταθερά. ὡς
ὡς  καὶ ἐπιλέγομε διαστήματα
καὶ ἐπιλέγομε διαστήματα 
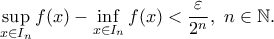
 στὰ
στὰ  .
.![x\in[0,1] x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ee73e01397b466fca4731317471bd6ff.png) , ὥστε
, ὥστε  , ὑπάρχει
, ὑπάρχει  , ὥστε
, ὥστε

 ,
,  ,
,  ,
, ![x\in [0,1]\setminus A x\in [0,1]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/7d0f8a051003b9076ea3a019ebabd8bc.png) , ἀποτελοῦν ἀνοικτὸ κάλυμμα τοῦ συμπαγοῦς
, ἀποτελοῦν ἀνοικτὸ κάλυμμα τοῦ συμπαγοῦς ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) . Ἄρα ὑπάρχει πεπερασμένο ὑποκάλυμμα:
. Ἄρα ὑπάρχει πεπερασμένο ὑποκάλυμμα:  . Διατάσσομε τὰ
. Διατάσσομε τὰ  , (
, (![K_1=[0,s_1),\,K_n=(r_n,1] K_1=[0,s_1),\,K_n=(r_n,1]](/forum/ext/geomar/texintegr/latexrender/pictures/993fdd9f3b8e12eef322b4a3f5694bf2.png) ), ὥστε:
), ὥστε:
 , τὰ ὁποῖα προκύπτουν ἀνωτέρω μὲ ἄκρα διαδοχικὰ σημεῖα
, τὰ ὁποῖα προκύπτουν ἀνωτέρω μὲ ἄκρα διαδοχικὰ σημεῖα  καὶ
καὶ 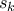 , ἰσχύουν τὰ ἑξῆς:
, ἰσχύουν τὰ ἑξῆς:![\displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big).
} \displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big).
}](/forum/ext/geomar/texintegr/latexrender/pictures/6648076ab2ef0f11f9d6b1176dc1e314.png)
 εἴτε εἶναι ὑποσύνολα διαστημάτων
εἴτε εἶναι ὑποσύνολα διαστημάτων  εἴτε ὑποσύνολα διαστημάτων
εἴτε ὑποσύνολα διαστημάτων  . Συνεπῶς τόσο ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν
. Συνεπῶς τόσο ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν  ποὺ εἶναι ὑποσύνολα διαστημάτων
ποὺ εἶναι ὑποσύνολα διαστημάτων  , ὅσο καὶ ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν
, ὅσο καὶ ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν  ποὺ εἶναι ὑποσύνολα διαστημάτων
ποὺ εἶναι ὑποσύνολα διαστημάτων  εἶναι λιγότερη ἀπὸ
εἶναι λιγότερη ἀπὸ  . Ἄρα
. Ἄρα![\displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big)<2\varepsilon.
} \displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big)<2\varepsilon.
}](/forum/ext/geomar/texintegr/latexrender/pictures/9254667211c17516891ed96d9cfea7f7.png)
 μη σταθερή, οπότε υπάρχουν
μη σταθερή, οπότε υπάρχουν  με
με  . Θα καταλήξουμε σε άτοπο.
. Θα καταλήξουμε σε άτοπο. μεταξύ τους με
μεταξύ τους με  . Επίσης επειδή
. Επίσης επειδή  αριθμήσιμο ενώ
αριθμήσιμο ενώ ![[c,d] [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c31d2b7df15fa7d119c2f8d13f69e10b.png) μη αριθμήσιμο, υπάρχει
μη αριθμήσιμο, υπάρχει ![\eta \in [c,d]-A \eta \in [c,d]-A](/forum/ext/geomar/texintegr/latexrender/pictures/5b66b752b43c8df720fdae046a1cb1a7.png) , και άρα
, και άρα  .
. παίρνει στο
παίρνει στο ![[c,d] [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c31d2b7df15fa7d119c2f8d13f69e10b.png) όλες τις τιμές (γνήσια) μεταξύ
όλες τις τιμές (γνήσια) μεταξύ  και
και  . Ειδικά οι τιμές αυτές είναι μη-μηδενικές. Με άλλα λόγια κάθε αριθμός μεταξύ του
. Ειδικά οι τιμές αυτές είναι μη-μηδενικές. Με άλλα λόγια κάθε αριθμός μεταξύ του  και του
και του  είναι της μορφής
είναι της μορφής  , από όπου συμπεραίνουμε ότι
, από όπου συμπεραίνουμε ότι  (διότι
(διότι  ). Αυτό όμως είναι άτοπο διότι
). Αυτό όμως είναι άτοπο διότι  αριθμήσιμο ενώ οι τιμές μεταξύ
αριθμήσιμο ενώ οι τιμές μεταξύ  και
και  είναι μη αριθμήσιμες το πλήθος. Και λοιπά.
είναι μη αριθμήσιμες το πλήθος. Και λοιπά. είναι παραγωγίσιμη και στο
είναι παραγωγίσιμη και στο  , πράγμα που δεν το δίνει η άσκηση. Άρα είναι ελλειπής. Έδειξα λοιπόν το ζητούμενο μόνο στην περίπτωση που η συνάρτηση είναι παντού παραγωγίσιμη.
, πράγμα που δεν το δίνει η άσκηση. Άρα είναι ελλειπής. Έδειξα λοιπόν το ζητούμενο μόνο στην περίπτωση που η συνάρτηση είναι παντού παραγωγίσιμη.Γεια σου Γιώργο.Γ.-Σ. Σμυρλής έγραψε: ↑Σάβ Ιούλ 06, 2019 11:08 pm
Τὰ ἀνοικτὰ διαστήματα,
,
,
, ἀποτελοῦν ἀνοικτὸ κάλυμμα τοῦ συμπαγοῦς
. Ἄρα ὑπάρχει πεπερασμένο ὑποκάλυμμα:
. Διατάσσομε τὰ
, (
), ὥστε:
Στὰ κλειστὰ διαστήματα, τὰ ὁποῖα προκύπτουν ἀνωτέρω μὲ ἄκρα διαδοχικὰ σημεῖα
καὶ
, ἰσχύουν τὰ ἑξῆς:
Τὰεἴτε εἶναι ὑποσύνολα διαστημάτων
εἴτε ὑποσύνολα διαστημάτων
. Συνεπῶς τόσο ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν
ποὺ εἶναι ὑποσύνολα διαστημάτων
, ὅσο καὶ ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν
ποὺ εἶναι ὑποσύνολα διαστημάτων
εἶναι λιγότερη ἀπὸ
. Ἄρα
![\displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big)<2\varepsilon.
} \displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big)<2\varepsilon.
}](/forum/ext/geomar/texintegr/latexrender/pictures/9254667211c17516891ed96d9cfea7f7.png)
 ,
,  ,
,  ,
, ![x\in [0,1]\setminus A x\in [0,1]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/7d0f8a051003b9076ea3a019ebabd8bc.png) , ἀποτελοῦν ἀνοικτὸ κάλυμμα τοῦ συμπαγοῦς
, ἀποτελοῦν ἀνοικτὸ κάλυμμα τοῦ συμπαγοῦς ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) . Ἄρα ὑπάρχει πεπερασμένο ὑποκάλυμμα:
. Ἄρα ὑπάρχει πεπερασμένο ὑποκάλυμμα:  +. Διατάσσομε τὰ
+. Διατάσσομε τὰ  , (
, (![K_1=[0,s_1),\,K_n=(r_n,1] K_1=[0,s_1),\,K_n=(r_n,1]](/forum/ext/geomar/texintegr/latexrender/pictures/993fdd9f3b8e12eef322b4a3f5694bf2.png) ), ὥστε:
), ὥστε: +
+ , τὰ ὁποῖα προκύπτουν ἀνωτέρω μὲ ἄκρα διαδοχικὰ σημεῖα
, τὰ ὁποῖα προκύπτουν ἀνωτέρω μὲ ἄκρα διαδοχικὰ σημεῖα  καὶ
καὶ  , +ἰσχύουν τὰ ἑξῆς:
, +ἰσχύουν τὰ ἑξῆς:![\displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big).
} \displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big).
}](/forum/ext/geomar/texintegr/latexrender/pictures/6648076ab2ef0f11f9d6b1176dc1e314.png)
 εἴτε εἶναι ὑποσύνολα διαστημάτων
εἴτε εἶναι ὑποσύνολα διαστημάτων  εἴτε ὑποσύνολα διαστημάτων
εἴτε ὑποσύνολα διαστημάτων  . Συνεπῶς τόσο ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν
. Συνεπῶς τόσο ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν  ποὺ εἶναι ὑποσύνολα διαστημάτων
ποὺ εἶναι ὑποσύνολα διαστημάτων  , ὅσο καὶ ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν
, ὅσο καὶ ἡ συνολικὴ συνεισφορὰ στὸ ἀνωτέρω τῶν  ποὺ εἶναι ὑποσύνολα διαστημάτων
ποὺ εἶναι ὑποσύνολα διαστημάτων  εἶναι λιγότερη ἀπὸ
εἶναι λιγότερη ἀπὸ  .
. ποὺ προκύπτουν από διαστήματα
ποὺ προκύπτουν από διαστήματα  εἶναι λιγότερη ἀπὸ
εἶναι λιγότερη ἀπὸ  +.
+.![\displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big)<3\varepsilon.
} \displaystyle{
\max_{x\in [0,1]}f(x)-\min_{x\in [0,1]}f(x)\le \sum_k \Big(\max_{x\in L_k}f(x)-\min_{x\in L_k}f(x)\Big)<3\varepsilon.
}](/forum/ext/geomar/texintegr/latexrender/pictures/d23b9a87cf2a3b6c1bb9651ba4225dac.png) +
+![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) τότε μπορούμε να πάρουμε κάποια από αυτά ώστε πάλι να το καλύπτουν και επιπλέον κάθε σημείο του
τότε μπορούμε να πάρουμε κάποια από αυτά ώστε πάλι να το καλύπτουν και επιπλέον κάθε σημείο του ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) βρίσκεται το πολύ σε δύο.
βρίσκεται το πολύ σε δύο.![f:[a,b]\rightarrow \mathbb{R} f:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/500b7d3e9c002fe33ef774ed310f6e88.png)
![A\subseteq [a,b] A\subseteq [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/1ebff311d3b87fca4e7a1256d964f352.png) αριθμήσιμο σύνολο.
αριθμήσιμο σύνολο.![x\in [a,b]-A x\in [a,b]-A](/forum/ext/geomar/texintegr/latexrender/pictures/42b89c0a2343abf13def40b114a47561.png)

 είναι αύξουσα.
είναι αύξουσα.

![\displaystyle B=\left \{ x\in (a,b]:f(a)\leq f(x)+\epsilon +\epsilon (x-a)+\epsilon \sum _{q_{n}<x}\frac{1}{2^{n}} \right \} \displaystyle B=\left \{ x\in (a,b]:f(a)\leq f(x)+\epsilon +\epsilon (x-a)+\epsilon \sum _{q_{n}<x}\frac{1}{2^{n}} \right \}](/forum/ext/geomar/texintegr/latexrender/pictures/dd5de0d5b1e3e325d60f0f3c9b75a762.png)


![B\subseteq [a,b] B\subseteq [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/414e8553c568d384195e9171e0a20a1c.png)





 (1)
(1) .
.
 .
.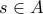

 με
με 

 και
και  ΑΤΟΠΟ
ΑΤΟΠΟ

 με
με


 και
και  ΑΤΟΠΟ.
ΑΤΟΠΟ.


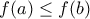 .
.
![[x,y] [x,y]](/forum/ext/geomar/texintegr/latexrender/pictures/8ca042e8ff30aba99a78e069db08b58a.png) προκύπτει ότι
προκύπτει ότι 
 είναι αύξουσα.
είναι αύξουσα.![x\in [a,b]-A x\in [a,b]-A](/forum/ext/geomar/texintegr/latexrender/pictures/42b89c0a2343abf13def40b114a47561.png)


 και η
και η  είναι αύξουσες που δίνει ότι η
είναι αύξουσες που δίνει ότι η  είναι σταθερή.
είναι σταθερή. , διὰ κάθε
, διὰ κάθε ![x\in [a,b]\setminus A x\in [a,b]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/c592a7e4468c4c3acccf359c17e7c741.png) , ὅπου
, ὅπου  ἀριθμήσιμο σύνολο, τότε
ἀριθμήσιμο σύνολο, τότε  αὔξουσα.
αὔξουσα.![c,d\in [a,b] c,d\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/768405dea1bf3697b134e29f5fb7355c.png) , μὲ
, μὲ  . Ἀρκεῖ νὰ δείξομε ὅτι
. Ἀρκεῖ νὰ δείξομε ὅτι 
 .
.  ὡς
ὡς  καὶ ἐπιλέγομε
καὶ ἐπιλέγομε  , ὥστε
, ὥστε
 . Τέτοια
. Τέτοια  's ὑπάρχουν χάριν τῆς συνεχείας τῆς
's ὑπάρχουν χάριν τῆς συνεχείας τῆς  . Θέτομε
. Θέτομε  . Ἰσχύει δὲ ὅτι
. Ἰσχύει δὲ ὅτι
![x\in [a,b]\setminus A x\in [a,b]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/c592a7e4468c4c3acccf359c17e7c741.png) . Τότε ὑπάρχει
. Τότε ὑπάρχει  , ὥστε
, ὥστε
 , καὶ
, καὶ  , ἔχομε ὅτι
, ἔχομε ὅτι
 , τελικῶς λαμβάνομε ὅτι
, τελικῶς λαμβάνομε ὅτι
 ἕνα πλῆρες κάλυμμα τοῦ
ἕνα πλῆρες κάλυμμα τοῦ ![[a, b] [a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/022022f289db140169cd9514f74ee648.png) , δηλαδὴ μία συλλογὴ κλειστῶν ὑποδιαστημάτων τοῦ
, δηλαδὴ μία συλλογὴ κλειστῶν ὑποδιαστημάτων τοῦ ![[a, b] [a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/022022f289db140169cd9514f74ee648.png) μὲ τὴν ἰδιότητα ὅτι διὰ κάθε
μὲ τὴν ἰδιότητα ὅτι διὰ κάθε ![x\in[a, b] x\in[a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/5e2126a8f8e1c5ea4e10e860fc09ed6a.png) , ὑπάρχει
, ὑπάρχει  , ὥστε ἡ
, ὥστε ἡ  νὰ περιλαμβάνει ὅλα τὰ κλειστὰ ὑποδιαστήματα τοῦ
νὰ περιλαμβάνει ὅλα τὰ κλειστὰ ὑποδιαστήματα τοῦ ![[a, b] [a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/022022f289db140169cd9514f74ee648.png) τὰ ὁποῖα περιέχουν τὸ
τὰ ὁποῖα περιέχουν τὸ  καὶ ἔχουν μῆκος μικρότερο τοῦ
καὶ ἔχουν μῆκος μικρότερο τοῦ  . Τότε ὑπάρχει διαμέριση
. Τότε ὑπάρχει διαμέριση 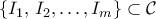 τοῦ
τοῦ ![[a, b] [a, b]](/forum/ext/geomar/texintegr/latexrender/pictures/022022f289db140169cd9514f74ee648.png) , ὅπου
, ὅπου ![I_i=[x_{i-1}, x_i] I_i=[x_{i-1}, x_i]](/forum/ext/geomar/texintegr/latexrender/pictures/4c3dcb48463b1e885cfec66bc15aa4ec.png) καὶ
καὶ  διὰ κάθε
διὰ κάθε  .
. τὴν συλλογὴ τῶν κλειστὼν ὑποδιαστημάτων
τὴν συλλογὴ τῶν κλειστὼν ὑποδιαστημάτων  τοῦ
τοῦ ![[c,d] [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c31d2b7df15fa7d119c2f8d13f69e10b.png) , ὥστε εἴτε
, ὥστε εἴτε  καὶ
καὶ  , γιὰ κάποιο
, γιὰ κάποιο  εἴτε
εἴτε  καὶ
καὶ  , γιὰ κάποιο
, γιὰ κάποιο ![x\in [a,b]\setminus A x\in [a,b]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/c592a7e4468c4c3acccf359c17e7c741.png) . Τὸ Λῆμμα τοῦ Cousin παρέχει τὴν ὕπαρξη σημείων
. Τὸ Λῆμμα τοῦ Cousin παρέχει τὴν ὕπαρξη σημείων  , ὥστε τὰ κλειστὰ διαστήματα
, ὥστε τὰ κλειστὰ διαστήματα![\displaystyle{
K_1=[x_0,x_1],\, K_2=[x_1,x_2],\ldots,K_m=[x_{m-1},x_m]
} \displaystyle{
K_1=[x_0,x_1],\, K_2=[x_1,x_2],\ldots,K_m=[x_{m-1},x_m]
}](/forum/ext/geomar/texintegr/latexrender/pictures/3d9c29184a9d5fbba039df5566292bb4.png)
 .
.  , ἕκαστον τῶν
, ἕκαστον τῶν  ἀποτελεῖ ὑποδιάστημα κάποιου διαστήματος
ἀποτελεῖ ὑποδιάστημα κάποιου διαστήματος  ἢ κάποιου διαστήματος
ἢ κάποιου διαστήματος  καὶ βεβαίως δύναται νὰ ἀποτελεῖ ὑποδιάστημα περισσοτέρων τοῦ ἑνός τέτοιων διαστημάτων. Διὰ κάθε τέτοιο
καὶ βεβαίως δύναται νὰ ἀποτελεῖ ὑποδιάστημα περισσοτέρων τοῦ ἑνός τέτοιων διαστημάτων. Διὰ κάθε τέτοιο  ἐπιλέγομε ἀκριβῶς ἕνα τέτοιο διάστημα. Συνεπῶς σὲ κάθε
ἐπιλέγομε ἀκριβῶς ἕνα τέτοιο διάστημα. Συνεπῶς σὲ κάθε  ἔχει ἀντιστοιχισθεῖ εἴτε μοναδικὸ
ἔχει ἀντιστοιχισθεῖ εἴτε μοναδικὸ  , ὥστε
, ὥστε  , τὸ ὁποῖο συμβολίζομε ὡς
, τὸ ὁποῖο συμβολίζομε ὡς  , εἴτε μοναδικὸ
, εἴτε μοναδικὸ ![x\in [a,b]\setminus A x\in [a,b]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/c592a7e4468c4c3acccf359c17e7c741.png) , ὥστε
, ὥστε  . Ἡ ἀπεικόνιση αὐτὴ δὲν εἶναι ἀπαραιτήτως 1-1, καθὼς ἂν τὸ
. Ἡ ἀπεικόνιση αὐτὴ δὲν εἶναι ἀπαραιτήτως 1-1, καθὼς ἂν τὸ  ἀποτελεῖ τὸ κοινὸ ἄκρο τῶν
ἀποτελεῖ τὸ κοινὸ ἄκρο τῶν  καὶ
καὶ  , τότε ἐνδέχεται νὰ ἰσχύει
, τότε ἐνδέχεται νὰ ἰσχύει  . Δήλαδὴ κάποια ἐκ τῶν διαστημάτων
. Δήλαδὴ κάποια ἐκ τῶν διαστημάτων  ἐνδέχεται νὰ ἔχουν ληφθεῖ ἔως καὶ δύο φορές.
ἐνδέχεται νὰ ἔχουν ληφθεῖ ἔως καὶ δύο φορές.  ὡς τὴν ἕνωση τῶν ξένων μεταξὺ τους συνόλων. Τοῦ
ὡς τὴν ἕνωση τῶν ξένων μεταξὺ τους συνόλων. Τοῦ  , τὸ ὁποῖο ἀποτελεῖται ἀπὸ τὰ
, τὸ ὁποῖο ἀποτελεῖται ἀπὸ τὰ  γιὰ τὰ ὁποῖα ἔχει ἐπιλεγεῖ
γιὰ τὰ ὁποῖα ἔχει ἐπιλεγεῖ  , ὥστε
, ὥστε  καὶ τοῦ
καὶ τοῦ  . Ἄν
. Ἄν  , τότε ἔχει ἐπιλεγεῖ κάποιο
, τότε ἔχει ἐπιλεγεῖ κάποιο ![x\in [a,b]\setminus A x\in [a,b]\setminus A](/forum/ext/geomar/texintegr/latexrender/pictures/c592a7e4468c4c3acccf359c17e7c741.png) , ὥστε
, ὥστε  .
. καὶ
καὶ  , τότε ἡ
, τότε ἡ  παρέχει ὅτι
παρέχει ὅτι
 , τότε ἡ
, τότε ἡ  παρέχει ὅτι
παρέχει ὅτι 



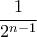 δύναται νὰ ἐμφανίζεται μηδέν, μία ἤ δύο (τὸ πολὺ) φορὲς ἂν τὸ
δύναται νὰ ἐμφανίζεται μηδέν, μία ἤ δύο (τὸ πολὺ) φορὲς ἂν τὸ  ἀποτελεῖ ἄκρο δύο ἐκ τῶν
ἀποτελεῖ ἄκρο δύο ἐκ τῶν  's.
's.  ἀριθμήσιμο σύνολο" ἀντικατασταθεῖ ἀπὸ τὴν ὑπόθεση "
ἀριθμήσιμο σύνολο" ἀντικατασταθεῖ ἀπὸ τὴν ὑπόθεση " σύνολο μηδενικοῦ μέτρου", τότε τὸ συμπέρασμα παύει νὰ ἰσχύει. Ἀντιπαράδειγμα: ἡ συνάρτηση Cantor. (Βλέπε [2]).
σύνολο μηδενικοῦ μέτρου", τότε τὸ συμπέρασμα παύει νὰ ἰσχύει. Ἀντιπαράδειγμα: ἡ συνάρτηση Cantor. (Βλέπε [2]).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες