 πολυώνυμο το οποίο δεν είναι ταυτοτικά
πολυώνυμο το οποίο δεν είναι ταυτοτικά  . Δείξτε ότι η εξίσωση
. Δείξτε ότι η εξίσωση  έχει τουλάχιστον μία πραγματική λύση.
έχει τουλάχιστον μία πραγματική λύση.Υποθέτω στόχος μας είναι να φτιάξουμε μια συνάρτηση
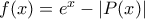 , η οποία είναι συνεχής και να βρούμε ένα
, η οποία είναι συνεχής και να βρούμε ένα  για το οποίο είναι η
για το οποίο είναι η  αρνητική, και άλλο ένα για το οποίο είναι θετική. Άρα αναγκαστικά θα υπάρχει κάποιο
αρνητική, και άλλο ένα για το οποίο είναι θετική. Άρα αναγκαστικά θα υπάρχει κάποιο  τέτοιο ώστε
τέτοιο ώστε 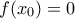 .
. Το όριο όταν
 είναι
είναι  Το όριο όταν
Το όριο όταν  είναι
είναι  και το
και το  είναι
είναι  , άρα εφαρμόζοντας Del'Hospital τόσες φορές όσες ο βαθμός του πολυωνύμου θα πάρουμε στο τέλος ότι
, άρα εφαρμόζοντας Del'Hospital τόσες φορές όσες ο βαθμός του πολυωνύμου θα πάρουμε στο τέλος ότι  οπότε
οπότε  . Άρα, αφού
. Άρα, αφού  συνεχής αναγκαστικά περνάει και από το
συνεχής αναγκαστικά περνάει και από το  άρα έχει αναγκαστικά τουλάχιστον μία πραγματική λύση. Είμαι σωστός; Κάποια άλλη προσέγγιση; Ευχαριστώ εκ των προτέρων!
άρα έχει αναγκαστικά τουλάχιστον μία πραγματική λύση. Είμαι σωστός; Κάποια άλλη προσέγγιση; Ευχαριστώ εκ των προτέρων!
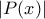 δεν είναι πάντα παραγωγίσιμο. Εύκολα διορθώνεται, αλλά το αφήνω χωρίς υπόδειξη για να το σκεφθείς.
δεν είναι πάντα παραγωγίσιμο. Εύκολα διορθώνεται, αλλά το αφήνω χωρίς υπόδειξη για να το σκεφθείς. . Κάνοντας χρήσεις του Κανόνα l'Hospital έχουμε
. Κάνοντας χρήσεις του Κανόνα l'Hospital έχουμε  όταν
όταν  . Ως εκ τούτου υπάρχει κάποιο
. Ως εκ τούτου υπάρχει κάποιο  τέτοιο ώστε
τέτοιο ώστε  για
για  .
. πολυώνυμο
πολυώνυμο 




 είναι
είναι 

