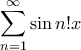

Να δειχθεί ότι υπάρχουν υπεραριθμήσιμο το πλήθος σημείων που συγκλίνει
καθώς και υπεραριθμήσιμο το πλήθος σημείων που αποκλίνει.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
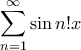

 όπου κάθε όρος είναι ίσος με
όπου κάθε όρος είναι ίσος με  ή
ή  με την επιπλέον συνθήκη ότι
με την επιπλέον συνθήκη ότι  αν
αν  σύνθετος. [Οι πρώτοι αριθμοί δεν παίζουν κανένα ρόλο. Επιλέξτε το αγαπημένο σας άπειρο υποσύνολο φυσικών
σύνθετος. [Οι πρώτοι αριθμοί δεν παίζουν κανένα ρόλο. Επιλέξτε το αγαπημένο σας άπειρο υποσύνολο φυσικών  για το οποίο
για το οποίο  αποκλίνει και θέστε
αποκλίνει και θέστε  για
για  .]
.]  Θα δείξω ότι η σειρά συγκλίνει απόλυτα για αυτό το
Θα δείξω ότι η σειρά συγκλίνει απόλυτα για αυτό το  .
. τότε
τότε  .
.  .
. τότε
τότε  .
.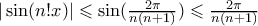 .
.
 . Όλες δίνουν διαφορετική τιμή του
. Όλες δίνουν διαφορετική τιμή του  όπως έχουμε δει και εδώ. Άρα έχουμε υπεραριθμήσιμα σημεία για τα οποία η σειρά συγκλίνει.
όπως έχουμε δει και εδώ. Άρα έχουμε υπεραριθμήσιμα σημεία για τα οποία η σειρά συγκλίνει. η επιπλέον συνθήκη γίνεται τώρα
η επιπλέον συνθήκη γίνεται τώρα  για
για  σύνθετο.
σύνθετο.  θα έχουμε
θα έχουμε 
 η ανισότητα Jordan δίνει
η ανισότητα Jordan δίνει  .
. θα έχουμε
θα έχουμε 
 .
.Τα παρακάτω είναι αντιφατικάDemetres έγραψε: ↑Παρ Δεκ 13, 2019 1:30 pmΈστω ακολουθίαόπου κάθε όρος είναι ίσος με
ή
με την επιπλέον συνθήκη ότι
αν
σύνθετος. [Οι πρώτοι αριθμοί δεν παίζουν κανένα ρόλο. Επιλέξτε το αγαπημένο σας άπειρο υποσύνολο φυσικών
για το οποίο
αποκλίνει και θέστε
για
.]
ΟρίζωΘα δείξω ότι η σειρά συγκλίνει απόλυτα για αυτό το
.
Αντότε
.
Τότε έχουμε.
Αντότε
.
Τότε έχουμε.
Άρα
Ασφαλώς υπάρχουν υπεραριθμήσιμες επιλογές για την ακολουθία. Όλες δίνουν διαφορετική τιμή του
όπως έχουμε δει και εδώ. Άρα έχουμε υπεραριθμήσιμα σημεία για τα οποία η σειρά συγκλίνει.
Με παρόμοιο τρόπο μπορούμε να βρούμε και υπεραριθμήσιμα σημεία για τα οποία η σειρά δεν συγκλίνει. Πιο συγκεκριμένα κάνουμε τις εξής αλλαγές:
Στηνη επιπλέον συνθήκη γίνεται τώρα
για
σύνθετο.
Γιαθα έχουμε
Γιαη ανισότητα Jordan δίνει
.
Γιαθα έχουμε
Τότε.
Είναι απλό τώρα ότι η σειρά αποκλίνει.
 όπου κάθε όρος είναι ίσος με
όπου κάθε όρος είναι ίσος με  ή
ή  με την επιπλέον συνθήκη ότι
με την επιπλέον συνθήκη ότι  αν
αν  σύνθετος. [Οι πρώτοι αριθμοί δεν παίζουν κανένα ρόλο. Επιλέξτε το αγαπημένο σας άπειρο υποσύνολο φυσικών
σύνθετος. [Οι πρώτοι αριθμοί δεν παίζουν κανένα ρόλο. Επιλέξτε το αγαπημένο σας άπειρο υποσύνολο φυσικών  για το οποίο
για το οποίο  αποκλίνει και θέστε
αποκλίνει και θέστε  για
για  .]
.] 
 αν το
αν το  δεν είναι τέλειο τετράγωνο και
δεν είναι τέλειο τετράγωνο και 
 οπότε αυτόματα το σύνολο που αποκλίνει είναι υπεραριθμήσιμο.
οπότε αυτόματα το σύνολο που αποκλίνει είναι υπεραριθμήσιμο. είναι το σύνολο που συγκλίνει τότε
είναι το σύνολο που συγκλίνει τότε 
 κλπ
κλπΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες