 είναι μια γραμμικη απεικόνιση. Ποια είναι η παραγωγος της
είναι μια γραμμικη απεικόνιση. Ποια είναι η παραγωγος της  ;
;Ξερω τι είναι γραμμικη απεικόνιση.
Επίσης ξερω οτι η παραγωγος
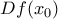 της
της  στο σημείο
στο σημείο  είναι ενας
είναι ενας  πινακας με τιμες
πινακας με τιμες  υπολογισμενες στο σημείο αυτό.
υπολογισμενες στο σημείο αυτό. Τι πρέπει να γράψω για να είναι σωστή η ασκηση;
Ευχαριστώ εκ των προτέρων

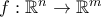 είναι σε κάθε σημείο
είναι σε κάθε σημείο  μια γραμμική απεικόνιση (με αντίστοιχο πίνακα με τιμές
μια γραμμική απεικόνιση (με αντίστοιχο πίνακα με τιμές 
 με πίνακα
με πίνακα  ισχύει
ισχύει 
 είναι διαφορίσιμη σε κάθε σημείο
είναι διαφορίσιμη σε κάθε σημείο  με παράγωγο
με παράγωγο  .
.

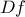 , είναι ο πίνακας
, είναι ο πίνακας  λύνοντας το όριο.
λύνοντας το όριο.