 τέτοια ώστε
τέτοια ώστε 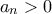 ,
,  ,
,  και
και ![\displaystyle{\lim_{n \rightarrow +\infty} \sqrt[n]{\prod_{k=1}^n{a_k}}=1} \displaystyle{\lim_{n \rightarrow +\infty} \sqrt[n]{\prod_{k=1}^n{a_k}}=1}](/forum/ext/geomar/texintegr/latexrender/pictures/91f68d5b21da4a524087f755fd523a3a.png) . Να δειχθεί ότι
. Να δειχθεί ότι  .
.Θα την έβαζα στο νέο φάκελο "Ασκήσεις ΜΟΝΟ για φοιτητές" αλλά τη θεωρώ δύσκολη.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 τέτοια ώστε
τέτοια ώστε 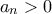 ,
,  ,
,  και
και ![\displaystyle{\lim_{n \rightarrow +\infty} \sqrt[n]{\prod_{k=1}^n{a_k}}=1} \displaystyle{\lim_{n \rightarrow +\infty} \sqrt[n]{\prod_{k=1}^n{a_k}}=1}](/forum/ext/geomar/texintegr/latexrender/pictures/91f68d5b21da4a524087f755fd523a3a.png) . Να δειχθεί ότι
. Να δειχθεί ότι  .
.
Tolaso J Kos έγραψε: ↑Παρ Φεβ 08, 2019 10:22 amΈστω ακολουθίατέτοια ώστε
,
,
και
. Να δειχθεί ότι
.
Θα την έβαζα στο νέο φάκελο "Ασκήσεις ΜΟΝΟ για φοιτητές" αλλά τη θεωρώ δύσκολη.





 (πεπερασμένο για κάθε
(πεπερασμένο για κάθε  και φραγμένο για κάθε
και φραγμένο για κάθε  και σταθερό
και σταθερό  )
)![\sqrt[n]{\prod_{k=1}^{n}a_k}=\sqrt[n]{\prod_{k\in f_\epsilon(n)}a_k}\sqrt[n]{\prod_{k\in g_\epsilon(n)}a_k}\sqrt[n]{\prod_{k\in S_n}a_k}\geq (1+\epsilon )^\frac{|f_\epsilon (n)|}{n}\cdot \sqrt[n]{\prod_{k\in f_\epsilon(n)}a_k}\sqrt[n]{\prod_{k\in S_n}a_k} \sqrt[n]{\prod_{k=1}^{n}a_k}=\sqrt[n]{\prod_{k\in f_\epsilon(n)}a_k}\sqrt[n]{\prod_{k\in g_\epsilon(n)}a_k}\sqrt[n]{\prod_{k\in S_n}a_k}\geq (1+\epsilon )^\frac{|f_\epsilon (n)|}{n}\cdot \sqrt[n]{\prod_{k\in f_\epsilon(n)}a_k}\sqrt[n]{\prod_{k\in S_n}a_k}](/forum/ext/geomar/texintegr/latexrender/pictures/3fabc6cc63807de93563458860e5b840.png)
![\geq (1+\epsilon )^\frac{|g_\epsilon (n)|}{n}(1-\epsilon )^\frac{|f_\epsilon (n)|}{n}\sqrt[n]{\prod_{k\in S_n}a_k} \geq (1+\epsilon )^\frac{|g_\epsilon (n)|}{n}(1-\epsilon )^\frac{|f_\epsilon (n)|}{n}\sqrt[n]{\prod_{k\in S_n}a_k}](/forum/ext/geomar/texintegr/latexrender/pictures/c38f4ac19fe316780bc728a0485a2a5e.png)
 φραγμένη στο
φραγμένη στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) από Bolzano Weierstrass υπάρχει υπακολουθία
από Bolzano Weierstrass υπάρχει υπακολουθία 

![\frac{|g_\epsilon (x_n)|}{x_n}\rightarrow a\in[0,1] \frac{|g_\epsilon (x_n)|}{x_n}\rightarrow a\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4f03598efbf4a2af54e548dacfee8f06.png)

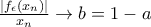
![\sqrt[x_n]{\prod_{k=1}^{n}a_{x_k}}\geq (1+\epsilon )^\frac{|g_\epsilon (x_n)|}{x_n}(1-\epsilon )^\frac{|f_\epsilon (x_n)|}{x_n}\sqrt[n]{\prod_{k\in S_n\cap x([n])}a_k} \rightarrow (1+\epsilon )^a(1-\epsilon )^b \sqrt[x_n]{\prod_{k=1}^{n}a_{x_k}}\geq (1+\epsilon )^\frac{|g_\epsilon (x_n)|}{x_n}(1-\epsilon )^\frac{|f_\epsilon (x_n)|}{x_n}\sqrt[n]{\prod_{k\in S_n\cap x([n])}a_k} \rightarrow (1+\epsilon )^a(1-\epsilon )^b](/forum/ext/geomar/texintegr/latexrender/pictures/0475e0981211f98378b43c0cc44a5f66.png)
![[n]=\left \{ 1,2,...,n \right \} [n]=\left \{ 1,2,...,n \right \}](/forum/ext/geomar/texintegr/latexrender/pictures/395ee30947eb3e99cd88e599ca52ee44.png)
![h(x)=(1+x)^a+(1-x)^b (x\in[0,1]) h(x)=(1+x)^a+(1-x)^b (x\in[0,1])](/forum/ext/geomar/texintegr/latexrender/pictures/10c05d2ce3b646ac25bc4f30d15ac8f9.png)
 και για
και για 

![\sqrt[x_n]{\prod_{k=1}^{n}a_{x_k}} \rightarrow s>1 \sqrt[x_n]{\prod_{k=1}^{n}a_{x_k}} \rightarrow s>1](/forum/ext/geomar/texintegr/latexrender/pictures/3b97240635f36636fef73241c7b1eecb.png) ΑΤΟΠΟ
ΑΤΟΠΟ και
και 
 τέτοια ώστε
τέτοια ώστε ![\frac{|g_\epsilon (x_n)|}{x_n} \rightarrow a\in[0,1] \frac{|g_\epsilon (x_n)|}{x_n} \rightarrow a\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e83427f8a8074bb9900e0308b8f7c9ee.png)
 δεν έχει σημεία συσσώρευσης στο
δεν έχει σημεία συσσώρευσης στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png)
 και
και 





Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες