
με τις ιδιότητες
Η
 είναι φθίνουσα και
είναι φθίνουσα και 
Υπάρχει
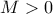 ώστε για κάθε
ώστε για κάθε  είναι
είναι 
Να δειχθεί ότι το ολοκλήρωμα

συγκλίνει
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

 είναι φθίνουσα και
είναι φθίνουσα και 
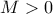 ώστε για κάθε
ώστε για κάθε  είναι
είναι 

Είναι σχεδόν άμεσο από το 2ο ΘΜΤΟΛ και το κριτήριο Cauchy. Απόδειξη το βράδυ.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Ιαν 26, 2019 7:39 pmΕστω
με τις ιδιότητες
Ηείναι φθίνουσα και
Υπάρχειώστε για κάθε
είναι
Να δειχθεί ότι το ολοκλήρωμα
συγκλίνει
 αν πάρουμε
αν πάρουμε  έχουμε
έχουμε 
 για τυχόν
για τυχόν  θα ισχύει τελικά
θα ισχύει τελικά 


ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Ιαν 26, 2019 7:39 pmΕστω
με τις ιδιότητες
Ηείναι φθίνουσα και
Υπάρχειώστε για κάθε
είναι
Να δειχθεί ότι το ολοκλήρωμα
συγκλίνει
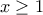 και
και 

 ολοκληρώσιμη ,άρα φραγμένη σε κάθε
ολοκληρώσιμη ,άρα φραγμένη σε κάθε  .
.


 τέτοιο ώστε
τέτοιο ώστε  και
και 


 θέτουμε
θέτουμε  και
και 

 φθίνουσα έχουμε ότι
φθίνουσα έχουμε ότι 
![f_{M_{i_{+}}},f_{M_{i_{-}}}\in [inff(\Delta _i),supf(\Delta_i)] f_{M_{i_{+}}},f_{M_{i_{-}}}\in [inff(\Delta _i),supf(\Delta_i)]](/forum/ext/geomar/texintegr/latexrender/pictures/2acf99922a0b8f74fb58978f2ae7a59a.png)
 και
και 


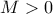 ώστε για κάθε
ώστε για κάθε  είναι
είναι  έχουμε
έχουμε 

 συγκλίνει .
συγκλίνει .


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 17 επισκέπτες