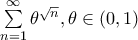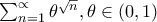
Σύγκλιση
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
Chatzibill
- Δημοσιεύσεις: 34
- Εγγραφή: Παρ Οκτ 05, 2018 4:53 pm
- Τοποθεσία: Αθήνα
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σύγκλιση
Γενικά,
(α) Για
 η σειρά αποκλίνει αφού ο γενικός όρος δε πάει στο
η σειρά αποκλίνει αφού ο γενικός όρος δε πάει στο  .
.(β) Όταν
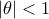 έχουμε:
έχουμε:
για κάποια θετική σταθερά
 και άρα η σειρά συγκλίνει απόλυτα. Το τελευταίο , διότι:
και άρα η σειρά συγκλίνει απόλυτα. Το τελευταίο , διότι: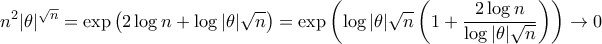
(γ) Για
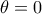 το άθροισμα προφανώς κάνει
το άθροισμα προφανώς κάνει  και άρα η σειρά συγκλίνει.
και άρα η σειρά συγκλίνει.Η φαντασία είναι σημαντικότερη από τη γνώση !


-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Σύγκλιση
Λίγο πιο απλά η βασική ανισότηταTolaso J Kos έγραψε: ↑Δευ Ιαν 07, 2019 10:30 pm
Γενικά,
(α) Γιαη σειρά αποκλίνει αφού ο γενικός όρος δε πάει στο
.
(β) Ότανέχουμε:

για κάποια θετική σταθεράκαι άρα η σειρά συγκλίνει απόλυτα. Το τελευταίο , διότι:
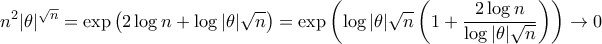
(γ) Γιατο άθροισμα προφανώς κάνει
και άρα η σειρά συγκλίνει.
Είναι

Αρα για

είναι
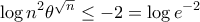
δηλαδή για

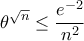
συμπλήρωμα.
ακόμα πιο απλά.
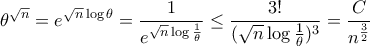
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες