 ακολουθία μέτρων πιθανότητας στον
ακολουθία μέτρων πιθανότητας στον  .
. Η
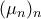 είναι tight (δε γνωρίζω την ελληνική ορολογία) αν για κάθε
είναι tight (δε γνωρίζω την ελληνική ορολογία) αν για κάθε 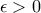 υπάρχει
υπάρχει  συμπαγές
συμπαγές  τέτοιο ώστε
τέτοιο ώστε  .
.Θέλω να δείξω ότι ικανή συνθήκη για να είναι η ακολουθία tight είναι η εξής :
υπάρχει
 συνεχής τέτοια ώστε
συνεχής τέτοια ώστε 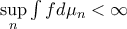 και
και  .
.Μια πιθανή αρχή θα ήταν χρησιμοποιώντας την ανισότητα markov για την f, δηλαδή
 και να θέσουμε
και να θέσουμε  . Το
. Το  είναι συμπαγές ως κλειστό( f είναι συνεχής ) και φραγμένο (λόγο του ορίου της f στο άπειρο) υποσύνολο του
είναι συμπαγές ως κλειστό( f είναι συνεχής ) και φραγμένο (λόγο του ορίου της f στο άπειρο) υποσύνολο του  . Μετά δε ξέρω πως να συνεχίσω.
. Μετά δε ξέρω πως να συνεχίσω.(αν και η ερώτηση αφορά μέτρα πιθανότητας προτιμώ να τη βάλω εδώ γιατί η λύση έχει μόνο επιχειρήματα ανάλυσης)
(Δεν είμαι απόλυτα σίγουρος ότι ισχύει το παραπάνω. Αν υπάρχει κάποιο αντιπαράδειγμα είναι ευπρόσδεκτο )

 και για σταθερό
και για σταθερό  θέτουμε
θέτουμε ?
? .
. .
. .
.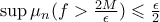 , όπου θέτοντας
, όπου θέτοντας  (συμπαγές ως κλειστό και φραγμένο υποσύνολο του
(συμπαγές ως κλειστό και φραγμένο υποσύνολο του  .
.