
Όριο με αφορμή
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Όριο με αφορμή
Τόλη γεια χαρά!Tolaso J Kos έγραψε: ↑Κυρ Δεκ 02, 2018 6:23 pmΜε αφορμή το ολοκλήρωμα εδώ καλείστε να υπολογίσετε το όριο:

Το όριο είναι
 Το αντιμετώπισα με στοιχειώδεις μεθόδους και οι πράξεις είναι πολλές.
Το αντιμετώπισα με στοιχειώδεις μεθόδους και οι πράξεις είναι πολλές.Όταν βρω χρόνο θα τις γράψω. Ουσιαστικά το όριο είναι το γνωστό ολοκλήρωμα

- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Όριο με αφορμή
Συμφωνώ ως προς το αποτέλεσμα. Έχω κάνει DCT και να πω και την αλήθεια ... πρέπει να έχω παραβιάσει όλα τα κριτήρια εδώ. Αλλά Calculus κάνουμε , οπότε όλα στέκουν αρκεί το αποτέλεσμα να είναι σωστό.
Λάμπρο αναμένω λύση.
Λάμπρο αναμένω λύση.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Όριο με αφορμή
Δεν στέκουν όλα. Πρέπει να ελέγχονται. Στην συγκεκριμένη περίπτωση δουλεύει το Θεώρημα Κυριαρχημένης Σύγκλισης αρκεί να εφαρμοστεί σωστά.
Ας γράψουμε Είναι απλό ότι αυτά τα ολοκληρώματα υπάρχουν. Κάνοντας την αντικατάσταση
Είναι απλό ότι αυτά τα ολοκληρώματα υπάρχουν. Κάνοντας την αντικατάσταση  παίρνουμε
παίρνουμε

Έστω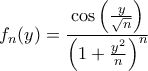 και
και 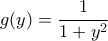
Η ακολουθία είναι αύξουσα. (*) Οπότε
είναι αύξουσα. (*) Οπότε  για κάθε
για κάθε  . Επιπλέον η
. Επιπλέον η  είναι ολοκληρώσιμη. (**) Οπότε από το Θεώρημα Κυριαρχημένης Σύγκλισης έχουμε
είναι ολοκληρώσιμη. (**) Οπότε από το Θεώρημα Κυριαρχημένης Σύγκλισης έχουμε

(*) Είναι

(**) Προσοχή: Δεν μπορούμε να πάρουμε διότι πρέπει
διότι πρέπει  .
.
Ας γράψουμε
 Είναι απλό ότι αυτά τα ολοκληρώματα υπάρχουν. Κάνοντας την αντικατάσταση
Είναι απλό ότι αυτά τα ολοκληρώματα υπάρχουν. Κάνοντας την αντικατάσταση  παίρνουμε
παίρνουμε
Έστω
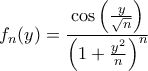 και
και 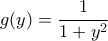
Η ακολουθία
 είναι αύξουσα. (*) Οπότε
είναι αύξουσα. (*) Οπότε  για κάθε
για κάθε  . Επιπλέον η
. Επιπλέον η  είναι ολοκληρώσιμη. (**) Οπότε από το Θεώρημα Κυριαρχημένης Σύγκλισης έχουμε
είναι ολοκληρώσιμη. (**) Οπότε από το Θεώρημα Κυριαρχημένης Σύγκλισης έχουμε
(*) Είναι

(**) Προσοχή: Δεν μπορούμε να πάρουμε
 διότι πρέπει
διότι πρέπει  .
.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Όριο με αφορμή
Το θέμα στην ουσία του δεν είναι υπολογιστικό.
Το είναι διακοσμητικό στοιχείο που μπερδεύει.
είναι διακοσμητικό στοιχείο που μπερδεύει.
Αν θέσουμε

τότε εύκολα μπορούμε να αποδείξουμε ότι

οπότε μπορούμε να εκφράσουμε το μέσω του
μέσω του 
Χρησιμοποιώντας το γινόμενο του Wallis και το προηγούμενο
μπορεί να αποδειχθεί ότι

Θέτουμε
οπότε λόγω του προηγούμενου είναι

Θα δείξουμε το εξής γενικότερο
Αν μετρήσιμη φραγμένη που είναι συνεχής στο
μετρήσιμη φραγμένη που είναι συνεχής στο 
τότε

ΑΠΟΔΕΙΞΗ
Εστω

υπάρχει

ώστε

Εχουμε

 (1)
(1)
το πρώτο ολοκλήρωμα είναι
 (2)
(2)
Για το δεύτερο έχουμε
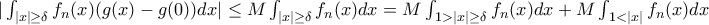
αλλά
 (3)
(3)
και
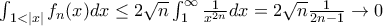 (4)
(4)
Λαμβάνοντας υπ οψιν τις (2),(3),(4) παίρνοντας
έχουμε αυτήν που θέλουμε
Το είναι το διπλάσιο του φράγματος της
είναι το διπλάσιο του φράγματος της  ενω
ενω
το είναι ένα ανω φράγμα της συγκλίνουσας ακολουθίας
είναι ένα ανω φράγμα της συγκλίνουσας ακολουθίας
 .
.
Φυσικά τα παραπάνω είναι γνωστές τεχνικές της Ανάλυσης.
Το
 είναι διακοσμητικό στοιχείο που μπερδεύει.
είναι διακοσμητικό στοιχείο που μπερδεύει.Αν θέσουμε

τότε εύκολα μπορούμε να αποδείξουμε ότι

οπότε μπορούμε να εκφράσουμε το
 μέσω του
μέσω του 
Χρησιμοποιώντας το γινόμενο του Wallis και το προηγούμενο
μπορεί να αποδειχθεί ότι

Θέτουμε

οπότε λόγω του προηγούμενου είναι

Θα δείξουμε το εξής γενικότερο
Αν
 μετρήσιμη φραγμένη που είναι συνεχής στο
μετρήσιμη φραγμένη που είναι συνεχής στο 
τότε

ΑΠΟΔΕΙΞΗ
Εστω

υπάρχει

ώστε

Εχουμε

 (1)
(1)το πρώτο ολοκλήρωμα είναι
 (2)
(2)Για το δεύτερο έχουμε
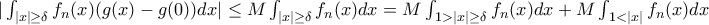
αλλά
 (3)
(3)και
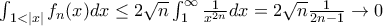 (4)
(4)Λαμβάνοντας υπ οψιν τις (2),(3),(4) παίρνοντας

έχουμε αυτήν που θέλουμε
Το
 είναι το διπλάσιο του φράγματος της
είναι το διπλάσιο του φράγματος της  ενω
ενωτο
 είναι ένα ανω φράγμα της συγκλίνουσας ακολουθίας
είναι ένα ανω φράγμα της συγκλίνουσας ακολουθίας  .
.Φυσικά τα παραπάνω είναι γνωστές τεχνικές της Ανάλυσης.
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Όριο με αφορμή
Η λύση που χρωστούσα με πιο στοιχειώδεις εργαλεία αλλά πολλές πράξεις.Tolaso J Kos έγραψε: ↑Κυρ Δεκ 02, 2018 6:23 pmΜε αφορμή το ολοκλήρωμα εδώ καλείστε να υπολογίσετε το όριο:

Θα ''χτυπήσουμε'' το ολοκλήρωμα στη καρδιά του δηλαδή σε μια περιοχή του μηδενός όπου έχει και την κύρια συνεισφορά.
Θα χρησιμοποιήσω τις παρακάτω κλασικές ανισότητες οι οποίες ισχύουν κοντά στο
 :
:


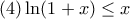
Καταρχάς κάνουμε την αλλαγή μεταβλητής όπως ο κ.Δημήτρης και παίρνουμε το
 .
.Αρκεί, λόγω συμμετρίας, να υπολογίσουμε το όριο του
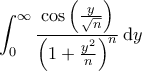 . Σπάμε το
. Σπάμε το 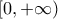 στα διαστήματα
στα διαστήματα ![[0,n^{\frac{1}{16}}] [0,n^{\frac{1}{16}}]](/forum/ext/geomar/texintegr/latexrender/pictures/f8f83e749827777157aec7e177b48809.png) ,
,  και θεωρούμε τα αντίστοιχα ολοκληρώματα. Στο πρώτο επειδή
και θεωρούμε τα αντίστοιχα ολοκληρώματα. Στο πρώτο επειδή ![y\in [0,n^{\frac{1}{16}}] y\in [0,n^{\frac{1}{16}}]](/forum/ext/geomar/texintegr/latexrender/pictures/596e96e80c81db61b2a1beef1f8dc4b2.png) για μεγάλα
για μεγάλα  θα είναι
θα είναι  οπότε κάνοντας χρήση των
οπότε κάνοντας χρήση των 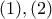 παίρνουμε
παίρνουμε  και
και 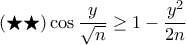
Για τον ίδιο λόγο με πριν θα είναι
 και από την
και από την  έχουμε
έχουμε 
 .
.Από την
 παίρνουμε
παίρνουμε 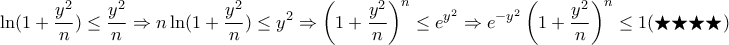
Συνδυάζοντας όλα τα αστεράκια παίρνουμε τελικά ότι


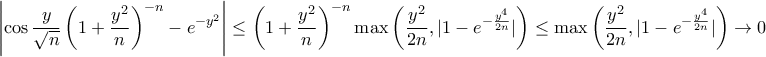
Άρα για
 παίρνουμε από την τελευταία
παίρνουμε από την τελευταία 
Μένει να δείξουμε ότι το
 είναι ασυμπτωτικά αμελητέο. Αυτό όμως είναι απλό αφού η εκθετική (για οποιαδήποτε βάση
είναι ασυμπτωτικά αμελητέο. Αυτό όμως είναι απλό αφού η εκθετική (για οποιαδήποτε βάση  )
) κυριαρχεί της πολυωνυμικής (οποιουδήποτε εκθέτη). Άρα για για αρκετά μεγάλο
 θα είναι
θα είναι Τελικά
Τελικά 
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Όριο με αφορμή
Δημήτρη,
όπως έχεις δει και συ στο
Προς Θεού δε λέω ότι δε πρέπει να ελέγχουμε τα πράματα αφού όπως λες και συ δε στέκουν όλα , αλλά από την άλλη ( τουλάχιστον για μένα ) το Calculus δεν είναι Θεωρητική Ανάλυση οπότε χρειάζεται λιγότερη αυστηρότητα αφού αν κάτι πάει στραβά αμέσως θα το καταλάβουμε. Εξαιρείται βέβαια η συμμετοχή σε διαγωνισμό όπου όταν καλούμαστε να υπολογίσουμε μια σειρά ή ένα ολοκλήρωμα πρέπει να τεκμηριώσουμε τα πάντα ( γιατί μπορούμε να κάνουμε αυτό, γιατί το άλλο ) αλλιώς θα χάσουμε μονάδες. Αλλά όταν κάνουμε Calculus για την δική μας ευχαρίστηση τότε ... τα πράματα απλουστεύουν κατά πολύ. Οποιαδήποτε άλλη γνώμη είναι δεκτή βέβαια.
Όσο για τη λύση έχω κάνει κάτι παρόμοιο με το δικό σου.
Σταύρο δε καταλαβαίνω γιατί τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Δεκ 03, 2018 11:27 pmΤο θέμα στην ουσία του δεν είναι υπολογιστικό.
Τοείναι διακοσμητικό στοιχείο που μπερδεύει.
 μπερδεύει. Συμφωνώ ότι δεν είναι και τόσο υπολογιστικό το θέμα. Όλα τα άλλα που γράφεις μου είναι κατανοητά.
μπερδεύει. Συμφωνώ ότι δεν είναι και τόσο υπολογιστικό το θέμα. Όλα τα άλλα που γράφεις μου είναι κατανοητά.Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Όριο με αφορμή
Tόλη, αυτό που εννοεί ο Σταύρος είναι ότι στην θέση τουTolaso J Kos έγραψε: ↑Τρί Δεκ 04, 2018 12:47 amΣταύρο δε καταλαβαίνω γιατί τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Δεκ 03, 2018 11:27 pmΤοείναι διακοσμητικό στοιχείο που μπερδεύει.
μπερδεύει.
 μπορεί να μπει οποιαδήποτε συνεχής φραγμένη
μπορεί να μπει οποιαδήποτε συνεχής φραγμένη συνάρτηση
 με
με  .
.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Όριο με αφορμή
Tolaso J Kos έγραψε: ↑Τρί Δεκ 04, 2018 12:47 amΔημήτρη,
όπως έχεις δει και συ στοστο Calculus μπορούμε να ορίσουμε τα πάντα, όπως κάναμε για παράδειγμα εδώ και δώσαμε νόημα σε τετραγωνική ρίζα αρνητικού αριθμού ώστε το αποτέλεσμα να είναι αισθητικά όμορφο. Στέκει από πλευράς πραγματικής; Όχι, αλλά δεν έχει καμία απολύτως σημασία αρκεί που το αποτέλεσμα είναι μαθητικά όμορφο. Πολλές φορές επίσης εναλλάσσουμε αθροίσματα με ολοκληρώματα ή και όρια χωρίς καν να ελέγξουμε αν επιτρέπεται αυτή η εναλλαγή ( έχουμε στο πίσω μέρος του κεφαλιού μας ότι η τεχνική αυτή θα δουλέψει στη πλειοψηφία των ασκήσεων ) .... και βγάζουμε σωστό αποτέλεσμα. Αν πάλι όλες οι τεχνικές αποτύχουν το DCT μας βγάζει από τη δύσκολη θέση ( όπως καλή ώρα εδώ ). Είναι η φύση του Calculus τέτοια που τα πράματα μιλάνε από μόνα τους. Δουλεύουν ; Οπότε όλα κυλούν ρολόι. Δε δουλεύουν; Βγάζουμε αλλοπρόσαλλα αποτελέσματα οπότε ξέρουμε ότι κάτι πάει λάθος και αλλάζουμε γραμμή πλεύσης.
Προς Θεού δε λέω ότι δε πρέπει να ελέγχουμε τα πράματα αφού όπως λες και συ δε στέκουν όλα , αλλά από την άλλη ( τουλάχιστον για μένα ) το Calculus δεν είναι Θεωρητική Ανάλυση οπότε χρειάζεται λιγότερη αυστηρότητα αφού αν κάτι πάει στραβά αμέσως θα το καταλάβουμε. Εξαιρείται βέβαια η συμμετοχή σε διαγωνισμό όπου όταν καλούμαστε να υπολογίσουμε μια σειρά ή ένα ολοκλήρωμα πρέπει να τεκμηριώσουμε τα πάντα ( γιατί μπορούμε να κάνουμε αυτό, γιατί το άλλο ) αλλιώς θα χάσουμε μονάδες. Αλλά όταν κάνουμε Calculus για την δική μας ευχαρίστηση τότε ... τα πράματα απλουστεύουν κατά πολύ. Οποιαδήποτε άλλη γνώμη είναι δεκτή βέβαια.
Όσο για τη λύση έχω κάνει κάτι παρόμοιο με το δικό σου.
Σταύρο δε καταλαβαίνω γιατί τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Δεκ 03, 2018 11:27 pmΤο θέμα στην ουσία του δεν είναι υπολογιστικό.
Τοείναι διακοσμητικό στοιχείο που μπερδεύει.
μπερδεύει. Συμφωνώ ότι δεν είναι και τόσο υπολογιστικό το θέμα. Όλα τα άλλα που γράφεις μου είναι κατανοητά.
Ειλικρινά δεν καταλαβαίνω.
Συγκεκριμένα.
Δηλαδή ότι είναι Μαθηματικά όμορφο είναι και σωστό;Tolaso J Kos έγραψε: ↑Τρί Δεκ 04, 2018 12:47 amΌχι, αλλά δεν έχει καμία απολύτως σημασία αρκεί που το αποτέλεσμα είναι μαθητικά όμορφο.
(υποθέτω ότι αντί μαθητικά ήθελες να γράψεις μαθηματικά)
Και που ξέρεις ότι το αποτέλεσμα είναι σωστό;Tolaso J Kos έγραψε: ↑Τρί Δεκ 04, 2018 12:47 amΠολλές φορές επίσης εναλλάσσουμε αθροίσματα με ολοκληρώματα ή και όρια χωρίς καν να ελέγξουμε αν επιτρέπεται αυτή η εναλλαγή ( έχουμε στο πίσω μέρος του κεφαλιού μας ότι η τεχνική αυτή θα δουλέψει στη πλειοψηφία των ασκήσεων ) .... και βγάζουμε σωστό αποτέλεσμα. Αν πάλι όλες οι τεχνικές αποτύχουν το DCT μας βγάζει από τη δύσκολη θέση ( όπως καλή ώρα εδώ ). Είναι η φύση του Calculus τέτοια που τα πράματα μιλάνε από μόνα τους. Δουλεύουν ; Οπότε όλα κυλούν ρολόι. Δε δουλεύουν; Βγάζουμε αλλοπρόσαλλα αποτελέσματα οπότε ξέρουμε ότι κάτι πάει λάθος και αλλάζουμε γραμμή πλεύσης.
Το βλέπεις με το μάτι;
Δηλαδή υπάρχει Θεωρητική Ανάλυση και άλλη Ανάλυση;
Συμφωνώ ότι όταν κάνουμε κάτι για την ευχαριστηση μας κάνουμε ότι θέλουμε για να το ευχαριστηθούμε.Αλλά αυτόTolaso J Kos έγραψε: ↑Τρί Δεκ 04, 2018 12:47 amΑλλά όταν κάνουμε Calculus για την δική μας ευχαρίστηση τότε ... τα πράματα απλουστεύουν κατά πολύ
σε καμία περίπτωση δεν σημαίνει ότι το κάναμε σωστά.
Και αν δεν κάνω λάθος το
Δυστυχώς τις παραπάνω απόψεις του Τόλη τις έχουν πολλοί.Μου έδωσε την αφορμή να απαντήσω
Το συγκεκριμένο θέμα νομίζω ότι φτιάχτηκε ως εξής:
Γνωρίζοντας ότι αν

τότε

(\delta η κατανομή του Dirac)
κοτσάραμε και ένα
 και το είπαμε άσκηση Calculus.
και το είπαμε άσκηση Calculus.Η προσωπική μου άποψη για τέτοιες κατασκευές είναι ότι δεν προάγουν τα Μαθηματικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Όριο με αφορμή
Αλλιώς.Tolaso J Kos έγραψε: ↑Κυρ Δεκ 02, 2018 6:23 pmΜε αφορμή το ολοκλήρωμα εδώ καλείστε να υπολογίσετε το όριο:

H αλλαγή μεταβλητής
 δίνει
δίνει  .
.Από την ανισότητα
 έχουμε
έχουμε  . Άρα
. Άρα 
Παίρνοντας όριο και με χρήση του τύπου του Stirling έχουμε ότι το αριστερό μέλος τείνει στο
 και το δεξί στο
και το δεξί στο 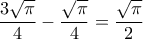 (ίσο με το προηγούμενο). Και λοιπά.
(ίσο με το προηγούμενο). Και λοιπά.Σχολιάζω ότι στην θέση του
 θα μπορούσε να μπει οποιαδήποτε άλλη συνάρτηση που ικανοποιεί την ανισότητα (ή κάποια παραλλαγή της) που χρησιμοποιήσαμε για το
θα μπορούσε να μπει οποιαδήποτε άλλη συνάρτηση που ικανοποιεί την ανισότητα (ή κάποια παραλλαγή της) που χρησιμοποιήσαμε για το  .
.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Όριο με αφορμή
Τόλη, νομίζω το κλειδί είναι εδώ. Μπορεί και να μην το καταλάβουμε καθόλου. Ιδίως αν δεν έχουμε στην διάθεσή μας κάποιο υπολογιστικό πακέτο. Π.χ.Tolaso J Kos έγραψε: ↑Τρί Δεκ 04, 2018 12:47 amοπότε χρειάζεται λιγότερη αυστηρότητα αφού αν κάτι πάει στραβά αμέσως θα το καταλάβουμε.
Να υπολογιστεί το

Αν περάσουμε αμέσως το όριο μέσα στο ολοκλήρωμα θα πάρουμε

που δεν θα μας υποψιάσει ότι κάτι κάναμε λάθος. Ακόμη και το ότι βρήκαμε απάντηση
 ενώ όλα τα ολοκληρώματα είναι θετικά δεν θα μας υποψιάζει ότι κάναμε λάθος διότι μπορεί τα ολοκληρώματα να μικραίνουν όταν το
ενώ όλα τα ολοκληρώματα είναι θετικά δεν θα μας υποψιάζει ότι κάναμε λάθος διότι μπορεί τα ολοκληρώματα να μικραίνουν όταν το  τείνει στο άπειρο.
τείνει στο άπειρο.Όμως κάθε ένα από αυτά τα ολοκληρώματα ισούται με
 . Πράγματι με αλλαγή μεταβλητών
. Πράγματι με αλλαγή μεταβλητών  έχουμε
έχουμε

Από την άλλη, κάτι που σίγουρα επιτρέπεται είναι αυτό που έκανε και ο Αρχιμήδης με την περίφημη ευρετική του μέθοδο:
Εύρεση του ποια πρέπει να είναι η απάντηση με οποιοδήποτε τρόπο και μετά επιβεβαίωση της ορθότητας με αυστηρό τρόπο. Π.χ. ο Αρχιμήδης πρώτα βρήκε πόσο πρέπει να ισούται το εμβαδόν κάτω από μια παραβολή με νόμους των μοχλών (την εξισορροπούσε σε μοχλό με ένα τρίγωνο) και έπειτα επιβεβαίωσε την απάντηση αυστηρά χρησιμοποιώντας την μέθοδό του της εξάντλησης.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες
