 να δείξετε ότι ισχύει
να δείξετε ότι ισχύει  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Αρχίζοντας από το δεξί μέλος, η αντικατάσταση
 δίνει ότι το ολοκλήρωμα ισούται
δίνει ότι το ολοκλήρωμα ισούται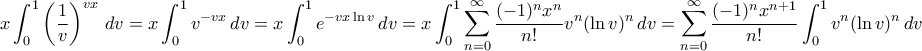
 και άρα, αναδρομικά,
και άρα, αναδρομικά, 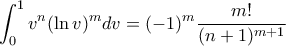 . Οπότε
. Οπότε  . Και λοιπά.
. Και λοιπά.Ευχαριστώ κ. Λάμπρου.Mihalis_Lambrou έγραψε: ↑Τρί Νοέμ 20, 2018 5:55 pmΑρχίζοντας από το δεξί μέλος, η αντικατάστασηδίνει ότι το ολοκλήρωμα ισούται
Tώρα το δεξί ολοκλήρωμα είναι γνώριμο. Βγαίνει με ολοκλήρωση κατά παράγοντες μέσω του
και άρα, αναδρομικά,
. Οπότε
. Και λοιπά.

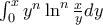 μπορεί να υπολογιστεί αναδρομικά. Θέτουμε
μπορεί να υπολογιστεί αναδρομικά. Θέτουμε 

 .
.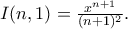 Άρα
Άρα 

.Mihalis_Lambrou έγραψε: ↑Τρί Νοέμ 20, 2018 5:55 pmTώρα το δεξί ολοκλήρωμα είναι γνώριμο. Βγαίνει με ολοκλήρωση κατά παράγοντες μέσω του
και άρα, αναδρομικά,
.
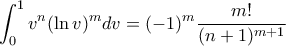 . Είναι σχεδόν μονολεκτικός και εξηγεί καλύτερα το "τι τρέχει", άσε που ισχύει γενικότερα για όχι κατ' ανάγκη ακέραιο
. Είναι σχεδόν μονολεκτικός και εξηγεί καλύτερα το "τι τρέχει", άσε που ισχύει γενικότερα για όχι κατ' ανάγκη ακέραιο  .
. . Παραγωγίζοντας ως προς
. Παραγωγίζοντας ως προς  με Leibnitz μέσα και έξω από το ολοκλήρωμα, έχουμε
με Leibnitz μέσα και έξω από το ολοκλήρωμα, έχουμε 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες