Όριο

Tolaso J Kos · #1

Να υπολογιστεί το όριο:

$\displaystyle{\ell = \lim_{x \rightarrow +\infty}\left(\sum_{n=1}^\infty\left(\frac xn\right)^n\right)^{1/x}}$

Λάμπρος Κατσάπας · #2

Tolaso J Kos έγραψε: ↑
Σάβ Νοέμ 17, 2018 1:49 am
Να υπολογιστεί το όριο:

$\displaystyle{\ell = \lim_{x \rightarrow +\infty}\left(\sum_{n=1}^\infty\left(\frac xn\right)^n\right)^{1/x}}$

$e^{\frac{1}{e}}$ . Η λύση αύριο.

1η ΛΥΣΗ

$\displaystyle{\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n=\int_{0}^{x}\left (\frac{x}{y} \right )^y dy=x \int_{0}^{1}\left \left ((\frac{1}{u} )^u \right )^x du}$ (στην τελευταία ισότητα έθεσα $u=\frac{y}{x}.$ )

Άρα

$\displaystyle{ \lim_{x\rightarrow +\infty }\left (\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n \right )^\frac{1}{x} = \lim_{x\rightarrow +\infty } \left (x \int_{0}^{1}\left \left ((\frac{1}{u} )^u \right )^x du \right )^\frac{1}{x} } \lim_{x\rightarrow +\infty }x^\frac{1}{x} \lim_{x\rightarrow +\infty } \left (\int_{0}^{1} \left ((\frac{1}{u} )^u \right )^xdu \right )^\frac{1}{x}$

$=1\cdot \underset{u\in (0,1]}{\sup((\frac{1}{u} )^u) }=e^\frac{1}{e}$

2η ΛΥΣΗ

Με πολλαπλασιασμό κατά μέλη στην $\displaystyle{ \left (1+\frac{1}{k} \right )^k<e<\left (1+\frac{1}{k} \right ) ^{k+1},k=1,2,...,n}$

παίρνουμε την $\displaystyle{(n-1)!e^{n-1}<n^n<n!e^n },n>1.$

Άρα για x>0

είναι $\displaystyle{\sum_{n=1}^{\infty } }\left (\frac{x}{n} \right )^n>\sum_{n=1}^{\infty } \frac{x^n}{n!e^n}=\sum_{n=1}^{\infty } \frac{(x/e)^n}{n!}=(e^{x/e}-1)$

και $\displaystyle{\sum_{n=1}^{\infty } }\left (\frac{x}{n} \right )^n<\sum_{n=1}^{\infty } \frac{x^n}{(n-1)!e^{n-1}}=x\sum_{n=1}^{\infty } \frac{(x/e)^{n-1}}{(n-1)!}=xe^{x/e}.$

Επίσης

$\lim_{x\rightarrow +\infty }\left (xe^{x/e} \right )^{1/x}=\lim_{x\rightarrow +\infty }\left (e^{x/e}-1 \right )^{1/x}=e^{1/e}.$

Άρα από ΚΠ $\displaystyle{ \lim_{x\rightarrow +\infty }\left (\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n \right )^\frac{1}{x} =e^{1/e} }$

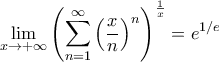
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #3

Λάμπρος Κατσάπας έγραψε: ↑
Σάβ Νοέμ 17, 2018 2:03 am

Tolaso J Kos έγραψε: ↑
Σάβ Νοέμ 17, 2018 1:49 am
Να υπολογιστεί το όριο:

$\displaystyle{\ell = \lim_{x \rightarrow +\infty}\left(\sum_{n=1}^\infty\left(\frac xn\right)^n\right)^{1/x}}$
$e^{\frac{1}{e}}$ . Η λύση αύριο.

1η ΛΥΣΗ

$\displaystyle{\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n=\int_{0}^{x}\left (\frac{x}{y} \right )^y dy=x \int_{0}^{1}\left \left ((\frac{1}{u} )^u \right )^x du}$ (στην τελευταία ισότητα έθεσα $u=\frac{y}{x}.$ )

Άρα

$\displaystyle{ \lim_{x\rightarrow +\infty }\left (\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n \right )^\frac{1}{x} = \lim_{x\rightarrow +\infty } \left (x \int_{0}^{1}\left \left ((\frac{1}{u} )^u \right )^x du \right )^\frac{1}{x} } \lim_{x\rightarrow +\infty }x^\frac{1}{x} \lim_{x\rightarrow +\infty } \left (\int_{0}^{1} \left ((\frac{1}{u} )^u \right )^xdu \right )^\frac{1}{x}$

$=1\cdot \underset{u\in (0,1]}{\sup((\frac{1}{u} )^u) }=e^\frac{1}{e}$

2η ΛΥΣΗ

Με πολλαπλασιασμό κατά μέλη στην $\displaystyle{ \left (1+\frac{1}{k} \right )^k<e<\left (1+\frac{1}{k} \right ) ^{k+1},k=1,2,...,n}$

παίρνουμε την $\displaystyle{(n-1)!e^{n-1}<n^n<n!e^n },n>1.$

Άρα για είναι $\displaystyle{\sum_{n=1}^{\infty } }\left (\frac{x}{n} \right )^n>\sum_{n=1}^{\infty } \frac{x^n}{n!e^n}=\sum_{n=1}^{\infty } \frac{(x/e)^n}{n!}=(e^{x/e}-1)$

και $\displaystyle{\sum_{n=1}^{\infty } }\left (\frac{x}{n} \right )^n<\sum_{n=1}^{\infty } \frac{x^n}{(n-1)!e^{n-1}}=x\sum_{n=1}^{\infty } \frac{(x/e)^{n-1}}{(n-1)!}=xe^{x/e}.$

Επίσης

$\lim_{x\rightarrow +\infty }\left (xe^{x/e} \right )^{1/x}=\lim_{x\rightarrow +\infty }\left (e^{x/e}-1 \right )^{1/x}=e^{1/e}.$

Άρα από ΚΠ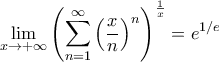 $\displaystyle{ \lim_{x\rightarrow +\infty }\left (\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n \right )^\frac{1}{x} =e^{1/e} }$

Την σχέση

$\displaystyle{\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n=\int_{0}^{x}\left (\frac{x}{y} \right )^y dy$

δεν την βλέπω

Είμαι περίεργος για το πώς προκύπτει.

Αντίθετα την

$\displaystyle{\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n=x \int_{0}^{1}\left \left ((\frac{1}{u} )^u \right )^x du}$

βλέπω πως μπορεί να προκύψει.

Λάμπρος Κατσάπας · #4

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Κυρ Νοέμ 18, 2018 7:57 pm

Την σχέση

$\displaystyle{\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n=\int_{0}^{x}\left (\frac{x}{y} \right )^y dy$

δεν την βλέπω

Είμαι περίεργος για το πώς προκύπτει.

Θα απαντήσω σε ξεχωριστή ανάρτηση. Έχει ενδιαφέρον νομίζω. Παρεμπιπτόντως η $\left(\frac{x}{y} \right )^y$

συμπεριφέρεται για μεγάλα

ως gaussian με συγκέντρωση τιμών γύρω από τη θέση μεγίστου $\frac{x}{e}$

και πρακτικά

αλλού. Γι'αυτό και το όριο προκύπτει $e^\frac{1}{e}$ , όσο θα βρίσκαμε δηλαδή αν απλά

θεωρούσαμε στο ολοκλήρωμα αντί της $\left(\frac{x}{y} \right )^y$ το max

της $e^\frac{x}{e}.$

Τώρα το πως το είδα. Αν παρατηρήσουμε τη σειρά προσεκτικά βλέπουμε ότι για n=1

η βάση της δύναμης είναι

ενώ για $n\rightarrow \infty$ η βάση πάει στο

. Επίσης για n< [x]

η βάση

είναι

οπότε αυξανουμένου του

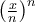η $\left (\frac{x}{n} \right )^n$ αυξάνεται ενώ για

n> [x]

μειώνεται αφού η βάση είναι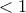

. Με αυτό το σκεπτικό είναι εμφανές νομίζω ότι υπέθεσα ότι η

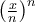$\left (\frac{x}{n} \right )^n$ συμπεριφέρεται σαν την $\left(\frac{x}{y} \right )^y$ και η σειρά της πρώτης

σαν το ολοκλήρωμα της δεύτερης από

έως

.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #5

Λάμπρος Κατσάπας έγραψε: ↑
Τρί Νοέμ 20, 2018 2:44 pm

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Κυρ Νοέμ 18, 2018 7:57 pm

Την σχέση

$\displaystyle{\sum_{n=1}^{\infty }\left (\frac{x}{n} \right )^n=\int_{0}^{x}\left (\frac{x}{y} \right )^y dy$

δεν την βλέπω

Είμαι περίεργος για το πώς προκύπτει.

Θα απαντήσω σε ξεχωριστή ανάρτηση. Έχει ενδιαφέρον νομίζω. Παρεμπιπτόντως η $\left(\frac{x}{y} \right )^y$

συμπεριφέρεται για μεγάλα ως gaussian με συγκέντρωση τιμών γύρω από τη θέση μεγίστου $\frac{x}{e}$

και πρακτικά αλλού. Γι'αυτό και το όριο προκύπτει $e^\frac{1}{e}$ , όσο θα βρίσκαμε δηλαδή αν απλά

θεωρούσαμε στο ολοκλήρωμα αντί της $\left(\frac{x}{y} \right )^y$ το της $e^\frac{x}{e}.$

Τώρα το πως το είδα. Αν παρατηρήσουμε τη σειρά προσεκτικά βλέπουμε ότι για η βάση της δύναμης είναι

ενώ για $n\rightarrow \infty$ η βάση πάει στο . Επίσης για η βάση

είναι οπότε αυξανουμένου του η $\left (\frac{x}{n} \right )^n$ αυξάνεται ενώ για

μειώνεται αφού η βάση είναι . Με αυτό το σκεπτικό είναι εμφανές νομίζω ότι υπέθεσα ότι η

$\left (\frac{x}{n} \right )^n$ συμπεριφέρεται σαν την $\left(\frac{x}{y} \right )^y$ και η σειρά της πρώτης

σαν το ολοκλήρωμα της δεύτερης από έως .

Η απάντηση δεν με καλύπτει.

Υπάρχει τρόπος να έχουμε αυτή την ισότητα;

Αλλο τα ασυμπτωτικά και άλλο η ισότητα.

#6

Είναι όντως ισότητα και ονομάζεται Sophomore's dream. (Σε αντιδιαστολή με το Freshman's dream.) Θέλει όμως κάποια δουλειά για να αποδειχθεί.

Η απόδειξη της περίπτωσης που περιγράφεται στην wikipedia δουλεύει και για την γενική περίπτωση που έχουμε εδώ. Την ειδική περίπτωση την έχουμε δει και εδώ.

Λάμπρος Κατσάπας · #7

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Νοέμ 20, 2018 8:44 pm

Η απάντηση δεν με καλύπτει.

Υπάρχει τρόπος να έχουμε αυτή την ισότητα;

Αλλο τα ασυμπτωτικά και άλλο η ισότητα.

H απάντηση δώθηκε εδώ viewtopic.php?f=9&t=63088.

Είπα ότι θα απαντήσω σε ξεχωριστή ανάρτηση και όπως φαίνεται στην εκφώνηση της παραπομπής αλλά και εδώ στην πρώτη λύση δεν αναφέρω πουθενά ότι η ισότητα ισχύει ασυμπτωτικά.

Ευχαριστώ τον Demetres για τις πληροφορίες. Δεν τις γνώριζα.

Όριο

Όριο

Re: Όριο

Re: Όριο

Re: Όριο

Re: Όριο

Re: Όριο

Re: Όριο

Μέλη σε σύνδεση