

[γιά τά οποία έχω επιλύσεις]
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 ...(εύκολο αυτό,τώρα αρχίζουν τα δύσκολα)
...(εύκολο αυτό,τώρα αρχίζουν τα δύσκολα) ,απ'όπου τώρα υπολογίζεται χωρίς δυσκολία...
,απ'όπου τώρα υπολογίζεται χωρίς δυσκολία... και να τη διασπάσει σε κλάσματα με παρονομαστές τους αντίστοιχους δευτεροβάθμιους παράγοντες, αλλά οι πράξεις που θα ακολουθήσουν είναι άνευ προηγουμένου...!! Φαντάζομαι θα υπάρχει κάποιος πιο έξυπνος τροπος...
και να τη διασπάσει σε κλάσματα με παρονομαστές τους αντίστοιχους δευτεροβάθμιους παράγοντες, αλλά οι πράξεις που θα ακολουθήσουν είναι άνευ προηγουμένου...!! Φαντάζομαι θα υπάρχει κάποιος πιο έξυπνος τροπος...Πράγματι υπάρχει.Κοτρώνης Αναστάσιος έγραψε: Φαντάζομαι θα υπάρχει κάποιος πιο έξυπνος τροπος...
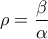 τό
τό  γίνεται
γίνεται 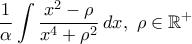 .
.
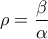 έχουμε
έχουμε 
 και να εξισώσει τους αντίστοιχους συντελεστές, να παρατηρήσει απλά ότι οι λύσεις τις
και να εξισώσει τους αντίστοιχους συντελεστές, να παρατηρήσει απλά ότι οι λύσεις τις  είναι οι
είναι οι  , οπότε θα είναι
, οπότε θα είναι 
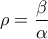 τό
τό  γίνεται
γίνεται  ,
,  .
.  , προκύπτουν
, προκύπτουν  καί
καί  .
. 
 .
.
 ,
, 
 .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: R BORIS και 15 επισκέπτες