![f:[0,1]\rightarrow \mathbb{R} f:[0,1]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/061d8197e20e9853f16cbd308ba889c8.png)
αύξουσα συνάρτηση.
Θέτουμε
 ,
, όπου

Νά δειχθεί ότι

όπου το
 είναι τέτοιο ώστε
είναι τέτοιο ώστε 
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![f:[0,1]\rightarrow \mathbb{R} f:[0,1]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/061d8197e20e9853f16cbd308ba889c8.png)
 ,
, 

 είναι τέτοιο ώστε
είναι τέτοιο ώστε 

 έχουμε
έχουμε  οπότε
οπότε  .
. έχουμε
έχουμε  .
.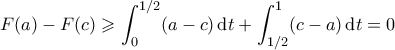

 έχει την συγκεκριμένη ιδιότητα.)
έχει την συγκεκριμένη ιδιότητα.)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες