
Όριο
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Όριο
Μπορούμε να αποφύγουμε τις  συναρτήσεις και Stirling δείχνοντας, π.χ. επαγωγικά, ότι
συναρτήσεις και Stirling δείχνοντας, π.χ. επαγωγικά, ότι

Το αφήνω ως άμεσο.
 συναρτήσεις και Stirling δείχνοντας, π.χ. επαγωγικά, ότι
συναρτήσεις και Stirling δείχνοντας, π.χ. επαγωγικά, ότι 
Το αφήνω ως άμεσο.
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Όριο
Γεια σου Τόλη !Ισπανικό είναι το όριο;
Το μερικό γινόμενο γράφεται
 Παίρνοντας λογάριθμο αρκεί να
Παίρνοντας λογάριθμο αρκεί να υπολογίσουμε το
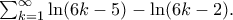 Κατά τα γνωστά είναι
Κατά τα γνωστά είναι
Όμως
 και επομένως
και επομένως 
Άρα

- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Όριο
Οπως ο Μιχάλης θέτουμε

Ειναι προφανές ότι η ακολουθία είναι γνησίως φθίνουσα και φραγμένη κάτω από το .
.
Αρκεί να αποκλίσουμε την περίπτωση
με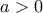 .
.
Αν ίσχυε αυτό τότε
Αλλά

Επειδή![(1-\frac{1}{4.2^{n}-\frac{2}{3}})^{2^{n}}\rightarrow \dfrac{1}{\sqrt[4]{e}} (1-\frac{1}{4.2^{n}-\frac{2}{3}})^{2^{n}}\rightarrow \dfrac{1}{\sqrt[4]{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/aae663271eeaf3136b47a9b193707aa5.png)
εχουμε ΑΤΟΠΟ

Ειναι προφανές ότι η ακολουθία είναι γνησίως φθίνουσα και φραγμένη κάτω από το
 .
.Αρκεί να αποκλίσουμε την περίπτωση

με
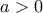 .
.Αν ίσχυε αυτό τότε

Αλλά

Επειδή
![(1-\frac{1}{4.2^{n}-\frac{2}{3}})^{2^{n}}\rightarrow \dfrac{1}{\sqrt[4]{e}} (1-\frac{1}{4.2^{n}-\frac{2}{3}})^{2^{n}}\rightarrow \dfrac{1}{\sqrt[4]{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/aae663271eeaf3136b47a9b193707aa5.png)
εχουμε ΑΤΟΠΟ
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Όριο
Μικρή παραλλαγή αυτής της λύσης: Εύκολα βλέπουμεMihalis_Lambrou έγραψε: ↑Τρί Οκτ 02, 2018 2:18 pmΜπορούμε να αποφύγουμε τιςσυναρτήσεις και Stirling δείχνοντας, π.χ. επαγωγικά, ότι

 . Πράγματι, με χρήση της
. Πράγματι, με χρήση της  έχουμε
έχουμε  που ισοδυναμεί με την αποδεικτέα.
που ισοδυναμεί με την αποδεικτέα. Πολλαπλασιάζοντας τώρα κατά μέλη την (*) για
 έως
έως  έχουμε τηλεσκοπικά
έχουμε τηλεσκοπικά  , και λοιπά.
, και λοιπά.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 15 επισκέπτες




