
Ξεκαθαρίζω ότι δεν γνωρίζω τη λύση της άσκησης!!!Μας ζητάει να βρούμε τους συντελεστές

Ιδέες δικιές μου...
Αν έχω υπολογίσει σωστά οι ρίζες του παρονομαστή είναι:
![\sqrt[3]{2}e^{i\pi } \sqrt[3]{2}e^{i\pi }](/forum/ext/geomar/texintegr/latexrender/pictures/a950e87462cfe41d16a95b900ac474b1.png) ,
, ![\sqrt[3]{2}e^{\frac{i\pi }{3}} \sqrt[3]{2}e^{\frac{i\pi }{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/53ff44d29e8cb588db2bd42a7f68ae17.png) ,
, ![\sqrt[3]{2}e^{\frac{i5\pi }{3}} \sqrt[3]{2}e^{\frac{i5\pi }{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/05fcc19564c229586945c9eec480a842.png) .
.Οι οποίες δεν μας εμποδίζουν στην ανάλυση της συνάρτησης σε δυναμοσειρά κοντά στο 0, αφού μπορούμε να δουλέψουμε σε κάποιο δισκάκι τοπικά!!!
Επίσης μάλλον κάπου θα χρειαστούμε τη γεωμετρική σειρά:

σκέφτηκα να θέσω:
 καθώς
καθώς ![\sqrt[3]{2}>\left | z \right |\Rightarrow \left | -\frac{z^3}{2} \right |<1 \sqrt[3]{2}>\left | z \right |\Rightarrow \left | -\frac{z^3}{2} \right |<1](/forum/ext/geomar/texintegr/latexrender/pictures/2f2ea417787f079e53a4f19ab0ec728f.png)
Απο κει και πέρα το χάος, καθώς μου εμφανίζεται σειρά της μορφής:
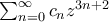 .
.Ευχαριστώ πολύ!!!

 .
. έχει κάποιους μηδενικούς συντελεστές που δεν βλέπω στην απάντηση σας.
έχει κάποιους μηδενικούς συντελεστές που δεν βλέπω στην απάντηση σας.
 και η
και η  έχουν την ίδια ακτίνας σύγκλισης? και αν ναι για ποιο λόγο?
έχουν την ίδια ακτίνας σύγκλισης? και αν ναι για ποιο λόγο?
![\sqrt[3]{2} \sqrt[3]{2}](/forum/ext/geomar/texintegr/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png) και τις δύο.
και τις δύο.


 .
. .
.![\large R=\left | i-\sqrt[3]{2}e^{\frac{i\pi }{3}} \right |=\sqrt{\sqrt[3]{2}\frac{1}{2}+(\sqrt[3]{2}\frac{\sqrt{3}}{2}-1)^2} \large R=\left | i-\sqrt[3]{2}e^{\frac{i\pi }{3}} \right |=\sqrt{\sqrt[3]{2}\frac{1}{2}+(\sqrt[3]{2}\frac{\sqrt{3}}{2}-1)^2}](/forum/ext/geomar/texintegr/latexrender/pictures/4e8ca57c9be77fe29fdc593ce573782a.png)