Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Tolaso J Kos · #1

Ας δηλώσουμε με $\mathcal{C}$ τη καμπύλη Viviani η οποία ορίζεται ως η τομή της σφαίρας $x^2+y^2+z^2=\alpha^2$ με το κύλινδρο $x^2+y^2=\alpha x$ . Να υπολογιστεί το ολοκλήρωμα:

$\displaystyle{\mathcal{J} = \oint \limits_{\mathcal{C}} y^2 \, \mathrm{d}x + z^2 \, \mathrm{d}y + x^2 \; \, \mathrm{d}z}$

#2

Κατ' αρχήν θέτω $\alpha=2p$ και, επομένως, η εξίσωση της σφαίρας είναι x^2+y^2+z^2=4p^2

και του κυλίνδρου είναι $\big\{(x-p)^2+y^2=p^2, \, z\in\mathbb{R} \big\}$ .

: viviani_c.png (30.03 KiB) Προβλήθηκε 1972 φορές

Μια παραμετρική παράσταση της καμπύλης

που είναι η τομή των δυο επιφανειών είναι $\overline{c}(t)=\big(p(\cos(2t)+1),\, p\sin(2t), \, 2p\sin{t}\big)\,, \; t\in[0,2\pi]$ .
Επομένως

$\begin{aligned} \displaystyle\mathop{\oint}\limits_{c}{y^2dx+z^2dy+x^2dz}&=\bigintsss_0^{2\pi}{\bigl(p^2\sin^2(2t),4p^2\sin{t},p^2(\cos(2t)+1)^2\bigr)\cdot\Bigl(p\frac{d}{dt}(\cos(2t)+1),\,p\frac{d}{dt}\sin(2t),\,2p\frac{d}{dt}\sin{t}\Bigr)\,dt}\\\noalign{\vspace{0.1cm}} &=p^3\bigintssss_0^{2\pi}{\bigl(\sin^2(2t),4\sin{t},(\cos(2t)+1)^2\bigr)\cdot\bigl(-2\sin(2t),\,2\cos(2t),\,2\cos{t}\bigr)\,dt}\\\noalign{\vspace{0.1cm}} &=8p^3\int_0^{2\pi}{2\sin{t}\cos^5{t}-2\sin {t} \cos^3{t}+\cos^5{t}-2\cos^4{t}+3\cos^2{t}-1 \,dt}\\\noalign{\vspace{0.1cm}} &=-4p^3\pi\,. \end{aligned}$

Παρατήρηση: Επειδή η καμπύλη είναι κλειστή, αν επιλεγεί μια παραμέτρησή της με αντίθετη φορά από αυτήν που επιλέχθηκε παραπάνω, το αποτέλεσμα θα ήταν $4p^3\pi$ .

Ας συνεχίσουμε την άσκηση με το εξής: Αν $B=\big\{(x,y,z)\in{\mathbb{R}}^3\;|\; x^2+y^2+z^2\leqslant4p^2\big\}$ η αντίστοιχη μπάλα και $K=\big\{(x,y,z)\in{\mathbb{R}}^3\;|\; (x-p)^2+y^2\leqslant p^2\big\}$ ο στερεός κύλινδρος, να βρεθεί ο όγκος του στερεού $\Sigma= B\cap K$ .

edit: 23:20, 16/8/18. Ο παραπάνω ζητούμενος όγκος δεν υπολογίζεται πλήρως αφού προκύπτει ελλειπτικό ολοκλήρωμα.

ttheodoros · #3

Μετασχηματίζουμε σε πολικές συντεταγμένες: $x=r \cos \theta, \, \, y=r \sin \theta$ .
Είναι $-\dfrac{\pi}{2} \leqslant \theta \leqslant \dfrac{\pi}{2}$ .

$\displaystyle{ x^2 + y^2 = 2 \rho x \, \Leftrightarrow \, r^2 = 2 \rho r \cos \theta \, \Leftrightarrow \, r = 2 \rho \cos \theta }$

$\displaystyle{ x^2 + y^2 + z^2= 4 \rho ^2 \, \Leftrightarrow \, r^2 +z^2= 4 \rho^2 \, \Leftrightarrow \, z = \sqrt{4 \rho^2 - r^2} }$

$V = \displaystyle{ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} \int_{-\sqrt{4 \rho^2 - r^2}}^{\sqrt{4 \rho^2 - r^2}} r\, \, dz \, dr \, d \theta } =4 \cdot \displaystyle{\int_{0}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} \int_{0}^{\sqrt{4 \rho^2 - r^2}} r\, \, dz \, dr \, d \theta } =4 \cdot \displaystyle{\int_{0}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} r \sqrt{4 \rho^2 - r^2}} \, dr \, d \theta }$

Παρατήρηση: Το ολοκλήρωμα υπολογίζεται.

Για $\rho=1$ το ολοκλήρωμα με χρήση του Wolfram Mathematica ισούται με $\dfrac{16}{9} \Big(3 \pi -4\Big)$ .

Για $\rho=3$ το ολοκλήρωμα με χρήση του Wolfram Mathematica ισούται με $4(36 \pi - 48)$ .

#4

ttheodoros έγραψε: ↑
Σάβ Αύγ 18, 2018 8:31 pm
... Παρατήρηση: Το ολοκλήρωμα υπολογίζεται. ...

Θεόδωρε,

είναι σωστή η παρατήρησή σου! Λόγω βιασύνης δεν είχα δει μια απλοποίηση και κατέληξα σε..ελλειπτικό ολοκλήρωμα. Διορθώνω λοιπόν...

Αν $D=\big\{(x,y)\in\mathbb{R}^2\;|\; (x-p)^2+y^2\leqslant p^2\big\}$ , τότε

$\begin{aligned} V(\Sigma)&=2\mathop{\iint}\limits_{D}\sqrt{4p^2-x^2-y^2}\;d(x,y)\\\noalign{\vspace{0.1cm}} &\stackrel{(*)}{=}2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_{0}^{2p\cos\theta}r\sqrt{4p^2-r^2}\; dr\,d\theta\\\noalign{\vspace{0.1cm}} &=-\frac{2}{3}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\big(4p^2-4p^2\cos^2\theta\big)^{\frac{3}{2}}-8p^3\,d\theta\\\noalign{\vspace{0.1cm}} &=\frac{16p^3}{3}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}1-|\sin\theta|^3\,d\theta\\\noalign{\vspace{0.1cm}} &=\frac{16p^3}{3}\Big(\pi-\frac{4}{3}\Big)\,. \end{aligned}$

(*)

Αλλαγή σε πολικές συντεταγμένες και $D=\big\{(r,\theta)\in\mathbb{R}^2\;|\; -\frac{\pi}{2}\leqslant \theta\leqslant \frac{\pi}{2} \,,\; 0\leqslant r\leqslant 2p\cos\theta\big\}$ .

#5

Ας συνεχίσουμε την άσκηση:

$B=\big\{(x,y,z)\in\mathbb{R}^3\;|\; x^2+y^2+z^2\leqslant4p^2\big\}$ , $K=\big\{(x,y,z)\in\mathbb{R}^3\;|\; (x-p)^2+y^2\leqslant p^2\big\}$ .

Έστω $S_{+}$ το άνω ημισφαίριο της σφαίρας $\partial B$ . Να υπολογισθεί το επιφανειακό ολοκλήρωμα

$\displaystyle\oiint\limits_{K\cap S_{+}}{(z,x,y)\cdot\overline{n}\, d\sigma}\,,$
όπου $\overline{n}$ ένα μοναδιαίο διάνυσμα, κάθετο στην επιφάνεια $K\cap S_{+}$ και τέτοιο ώστε να "κοιτάζει" προς το εξωτερικό της $K\cap S_{+}$ .

#6

grigkost έγραψε: ↑
Δευ Αύγ 20, 2018 3:22 am
Έστω $S_{+}$ το άνω ημισφαίριο της σφαίρας $\partial B$ . Να υπολογισθεί το επιφανειακό ολοκλήρωμα

$\displaystyle\oiint\limits_{K\cap S_{+}}{(z,x,y)\cdot\overline{n}\, d\sigma}\,,$
όπου $\overline{n}$ ένα μοναδιαίο διάνυσμα, κάθετο στην επιφάνεια $K\cap S_{+}$ και τέτοιο ώστε να "κοιτάζει" προς το εξωτερικό της $K\cap S_{+}$ .

Υπόδειξη:

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

ttheodoros · #7

Λύση 1

Μετασχηματίζουμε σε πολικές συντεταγμένες: $x=r \cos \theta, \, \, y=r \sin \theta$ .
Είναι $-\dfrac{\pi}{2} \leqslant \theta \leqslant \dfrac{\pi}{2}$ .

$\displaystyle{ x^2 + y^2 = 2 \rho x \, \Leftrightarrow \, r^2 = 2 \rho r \cos \theta \, \Leftrightarrow \, r = 2 \rho \cos \theta }$

$\displaystyle{ x^2 + y^2 + z^2= 4 \rho ^2 \, \Leftrightarrow \, r^2 +z^2= 4 \rho^2 \, \Leftrightarrow \, z = \sqrt{4 \rho^2 - r^2} }$

Θα βρούμε μια παραμετρική παράσταση $\vec{\Phi}$ της επιφάνειας $K\cap S_{+}$ :
$\displaystyle{ \vec{\Phi}: \, D \rightarrow \mathbb R^3, \qquad (r,\theta) \longmapsto \big(x(r,\theta), \, y(r,\theta),\, z(r,\theta)\big) }$

όπου, $D=\Big\{(r,\theta)|, \, \, r \in [0, 2 \rho \cos \theta ], \, \, \theta \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\Big\}$ και τα x, y, z

ορίζονται όπως πιο πάνω.

Μια παραμετρική παράσταση της επιφάνειας $\Phi=K\cap S_{+}$ είναι:

$\displaystyle{ \Phi(r, \theta)= r \cos \theta \vec{i} + r \sin \theta \vec{j} + \sqrt{4 \rho^2 - r^2} \vec{k}, \qquad -\dfrac{\pi}{2} \leqslant \theta \leqslant \dfrac{\pi}{2}, \quad 0 \leqslant r \leqslant 2 \rho \cos \theta }$

Είναι
$\displaystyle{ \dfrac{\partial \vec{\Phi}}{\partial r}(r,\theta)=\dfrac{\partial x}{\partial r}(r,\theta) \, \vec{i} + \dfrac{\partial y}{\partial r}(r,\theta) \, \vec{j} + \dfrac{\partial z}{\partial r}(r,\theta) \, \vec{k} =\cos \theta\, \vec{i} + \sin \theta \, \vec{j} - \dfrac{r}{\sqrt{4 \rho^2 - r^2}} \, \vec{k}, }$
και
$\displaystyle{ \dfrac{\partial \vec{\Phi}}{\partial \theta}(r,\theta)=\dfrac{\partial x}{\partial \theta}(r,\theta) \, \vec{i} + \dfrac{\partial y}{\partial \theta}(r,\theta) \, \vec{j} + \dfrac{\partial z}{\partial \theta}(r,\theta) \, \vec{k} =-r \sin \theta\, \vec{i} + r \cos \theta \, \vec{j} +0 \, \vec{k}. }$

$\displaystyle{ \vec{n}=\dfrac{\partial \vec{\Phi}}{\partial r}(r,\theta) \times \dfrac{\partial \vec{\Phi}}{\partial \theta}(r,\theta) = \det \begin{pmatrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & \frac{\partial z}{\partial u}\\ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta} \end{pmatrix} = \det \begin{pmatrix} \vec{i} & \vec{j} & \vec{k} \\ \cos \theta & \sin \theta & \dfrac{r}{\sqrt{4 \rho^2 - r^2}}\\ -r \sin \theta & r \cos \theta & 0 \end{pmatrix} }$

$\displaystyle{ = -\dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i} -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k} }$

Άρα,

$\displaystyle{ \iint \limits_{K\cap S_{+}}{(z,x,y)\cdot\overline{n}\, d\sigma} =\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} (\sqrt{4 \rho^2 - r^2}, r \cos \theta, r \sin \theta) \cdot ( -\dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}}, -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}}, r) \, dr d \theta }$

$\displaystyle{ =\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} (-r^2 \cos \theta -\dfrac{r^3 \cos \theta \sin \theta}{\sqrt{4 \rho^2 - r^2}} + r^2 \sin \theta) \, dr d \theta =\ldots = -\rho^3 \pi. }$

edit: 26/8/18, 20:00. Στην συγκεκριμένη δημοσίευση υπάρχουν υπολογιστικά λάθη, τα οποία διορθώθηκαν σε επόμενες δημοσιεύσεις.

ttheodoros · #8

Λύση 2

$\displaystyle{ \iint \limits_{K\cap S_{+}}{(z,x,y)\cdot\overline{n}\, d\sigma} = \iint \limits_{K\cap S_{+}}{\vec{F}\cdot \vec{n}\, d\sigma} }$
όπου $\vec{F}=(z,x,y)$ .

Είναι
$\displaystyle{ \iint \limits_{K\cap S_{+}}{\vec{F}\cdot \vec{n}\, d\sigma} =\iiint \limits_D div\vec{F} dV =2\int_{0}^{2 \rho} \int_{0}^{\sqrt{2 \rho x -x^2}} \int_{0}^{\sqrt{4 \rho^2 - x^2-y^2}} \dfrac{\partial z}{\partial x} \, dz dy dx }$

$\displaystyle{ =2\int_{0}^{2 \rho} \int_{0}^{\sqrt{2 \rho x -x^2}} \int_{0}^{\sqrt{4 \rho^2 - x^2-y^2}} -\dfrac{x}{\sqrt{4 \rho^2 - x^2-y^2}} \, dz dy dx=\ldots = -\rho^3 \pi. }$

edit: 26/8/18, 20:00. Η εφαρμογή του θεωρήματος απόκλισης δεν είναι σωστή. Βλέπε επόμενες δημοσιεύσεις.

#9

Ωραία, Θεόδωρε. Μια 3η λύση:

Παρατηρούμε ότι
$\begin{aligned} -\frac{1}{2}\,\big(\nabla\times \overline{F}\,\big)(x,y,z)=(z,y,x)\quad {(1)}\,. \end{aligned}$
Για το διανυσματικό πεδίο $\overline{F}$ , για την επιφάνεια $E_{+}=S_{+}\cap K,\quad(*)$ και για το θετικά προσανατολισμένο σύνορό της $c_{+}=\partial (E_{+})$ με παραμετρική παράσταση $\overline{c}_{+}(t)=\big(p(\cos(2t)+1),\, p\sin(2t), \, 2p\sin{t}\big)\,, \; t\in[0,\pi]$ , πληρούνται οι συνθήκες του θεωρήματος Stokes. Επομένως

$\begin{aligned} \displaystyle\oiint\limits_{E_{+}}{\big(\nabla\times\overline{F}\,\big)\cdot\overline{n}\, d\sigma}&=\ointctrclockwise\limits_{c_{+}}{\overline{F}\cdot d\overline{r}}\\\noalign{\vspace{0.1cm}} &\stackrel{(**)}{=\!=}-2p^3\pi\hspace{0.8cm}\Longrightarrow\\\noalign{\vspace{0.1cm}} \oiint\limits_{E_{+}}{(z,x,y)\cdot\overline{n}\, d\sigma}&\stackrel{(1)}{=}-\frac{1}{2}\,(-2p^3\pi)=p^3\pi\,. \end{aligned}$
(*)

Η παραμετρική παράσταση της $E_{+}$ θεωρείται ότι είναι τέτοια ώστε το κάθετο διάνυσμα $\overline{N}$ να βλέπει προς έξω (του τμήματος) της σφαίρας.
(**)

Προηγούμενο αποτέλεσμα.

: surf_integ.png (43.52 KiB) Προβλήθηκε 1595 φορές

Υ.Γ. Μπορεί η 1η λύση του Θεόδωρου να μοιάζει μακροσκελής, αλλά είναι αυτόνομη (και κλασσική).

ttheodoros · #10

Θα δείξουμε ότι το διάνυσμα $\vec{n} = -\dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i} -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k}$ που βρήκαμε πιο πάνω βλέπει προς το εξωτερικό της επιφάνειας.

Όταν $x=\rho, \, y=0$ τότε απο την εξίσωση $x^2+y^2+z^2 = 4 \rho^2$ βρίσκουμε $z=\sqrt{3} \rho$ αφού z>0

.

Το σημείο $A(\rho, 0, \sqrt{3} \rho)$ του τμήματος της σφαίρας αντιστοιχεί για $r=\rho, \, \theta=0$ .
Δηλαδή, $(\rho, 0, \sqrt{3} \rho) = \Phi(\rho,0)$ .

$\vec{n}(\rho, 0)= -\dfrac{\rho}{\sqrt{3}}\vec{i} + 0 \vec{j}+ \rho \vec{k}$ .

Παρατηρούμε ότι $\vec{n} \cdot \vec{k} = (-\dfrac{\rho}{\sqrt{3}}\vec{i} + 0 \vec{j}+ \rho \vec{k}) \cdot (0,0,1)= \rho>0$ .

Δηλαδή τα διανύσματα $\vec{n}$ και $\vec{k}$ σχηματίζουν οξεία γωνία μεταξύ τους και επομένως το διάνυσμα $\vec{n}$ βλέπει προς τα έξω (του τμήματος) της σφαίρας.

Διαφορετικά: Το διάνυσμα θέσης του σημείου

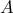του τμήματος της σφαίρας είναι $\overrightarrow{OA}= (\rho, 0, \sqrt{3} \rho)$ .

Επειδή $\overrightarrow{OA} \cdot \vec{n}= (\rho, 0, \sqrt{3} \rho)\cdot (-\dfrac{\rho}{\sqrt{3}}, 0, \rho)= -\dfrac{\rho^2}{\sqrt{3}} + \sqrt{3} \rho^2 >0$
τα διανύσματα $\overrightarrow{OA}$ και $\vec{n}$ σχηματίζουν οξεία γωνία μεταξύ τους και επομένως το διάνυσμα $\vec{n}$ βλέπει προς τα έξω (του τμήματος) της σφαίρας.

#11

ttheodoros έγραψε: ↑
Σάβ Αύγ 25, 2018 9:49 pm
Λύση 1
...Μια παραμετρική παράσταση της επιφάνειας $\Phi=K\cap S_{+}$ είναι:

$\displaystyle{ \Phi(r, \theta)= r \cos \theta \vec{i} + r \sin \theta \vec{j} + \sqrt{4 \rho^2 - r^2} \vec{k}, \qquad -\dfrac{\pi}{2} \leqslant \theta \leqslant \dfrac{\pi}{2}, \quad 0 \leqslant r \leqslant 2 \rho \cos \theta }$

Είναι
$\displaystyle{ \dfrac{\partial \vec{\Phi}}{\partial r}(r,\theta)=\dfrac{\partial x}{\partial r}(r,\theta) \, \vec{i} + \dfrac{\partial y}{\partial r}(r,\theta) \, \vec{j} + \dfrac{\partial z}{\partial r}(r,\theta) \, \vec{k} =\cos \theta\, \vec{i} + \sin \theta \, \vec{j} - \dfrac{r}{\sqrt{4 \rho^2 - r^2}} \, \vec{k}, }$
και
$\displaystyle{ \dfrac{\partial \vec{\Phi}}{\partial \theta}(r,\theta)=\dfrac{\partial x}{\partial \theta}(r,\theta) \, \vec{i} + \dfrac{\partial y}{\partial \theta}(r,\theta) \, \vec{j} + \dfrac{\partial z}{\partial \theta}(r,\theta) \, \vec{k} =-r \sin \theta\, \vec{i} + r \cos \theta \, \vec{j} +0 \, \vec{k}. }$

$\displaystyle{ \vec{n}=\dfrac{\partial \vec{\Phi}}{\partial r}(r,\theta) \times \dfrac{\partial \vec{\Phi}}{\partial \theta}(r,\theta) = \det \begin{pmatrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & \frac{\partial z}{\partial u}\\ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta} \end{pmatrix} = \det \begin{pmatrix} \vec{i} & \vec{j} & \vec{k} \\ \cos \theta & \sin \theta &{\color{red}?} \dfrac{r}{\sqrt{4 \rho^2 - r^2}}\\ -r \sin \theta & r \cos \theta & 0 \end{pmatrix} }$

$\displaystyle{ ={\color{red}-}\dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i}\, {\color{red}-}\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k} }$

Άρα,...

Έχει "διαφύγει¨ένα μείον στο υπολογισμό του καθέτου (σημειωμένα με κόκκινο). Είναι

$\overline{N}=\displaystyle\frac{r^2\cos\theta}{\sqrt{4p^2-r^2}}\,{\overline{e}_1}+\frac{r^2\sin\theta}{\sqrt{4p^2-r^2}}\,{\overline{e}_2} +r\,{\overline{e}_3}$
Αυτό το κάθετο "βλέπει" προς το εξωτερικό της επιφάνειας και το αντίστοιχο επιφανειακό ολοκλήρωμα ισούται με $p^3\pi$ .

ttheodoros έγραψε: ↑
Κυρ Αύγ 26, 2018 8:33 pm
Θα δείξουμε ότι το διάνυσμα $\vec{n} = -\dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i} -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k}$ που βρήκαμε πιο πάνω βλέπει προς το εξωτερικό της επιφάνειας.....

Επομένως το διάνυσμα $\vec{n} = -\dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i} -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k}$ δεν είναι κάθετο.

ttheodoros · #12

Γρηγόρη έχεις δίκαιο ότι μου διέφυγε ένα "-" στην δεύτερη γραμμή της ορίζουσας (εκεί που έβαλες "?")

Επομένως το κάθετο διάνυσμα θα είναι

$\displaystyle{ \vec{n}= \dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i} {\color{red}-}\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k} }$

ttheodoros · #13

Πιο κάτω βάζω διορθωμένη την Λύση 1. Ευχαριστώ και δημόσια τον Γρηγόρη Κωστάκο για τις παρατηρήσεις του.

Μετασχηματίζουμε σε πολικές συντεταγμένες: $x=r \cos \theta, \, \, y=r \sin \theta$ .
Είναι $-\dfrac{\pi}{2} \leqslant \theta \leqslant \dfrac{\pi}{2}$ .

$\displaystyle{ x^2 + y^2 = 2 \rho x \, \Leftrightarrow \, r^2 = 2 \rho r \cos \theta \, \Leftrightarrow \, r = 2 \rho \cos \theta }$

$\displaystyle{ x^2 + y^2 + z^2= 4 \rho ^2 \, \Leftrightarrow \, r^2 +z^2= 4 \rho^2 \, \Leftrightarrow \, z = \sqrt{4 \rho^2 - r^2} }$

Θα βρούμε μια παραμετρική παράσταση $\vec{\Phi}$ της επιφάνειας $K\cap S_{+}$ :
$\displaystyle{ \vec{\Phi}: \, D \rightarrow \mathbb R^3, \qquad (r,\theta) \longmapsto \big(x(r,\theta), \, y(r,\theta),\, z(r,\theta)\big) }$

όπου, $D=\Big\{(r,\theta)|, \, \, r \in [0, 2 \rho \cos \theta ], \, \, \theta \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\Big\}$ και τα x, y, z

ορίζονται όπως πιο πάνω.

Μια παραμετρική παράσταση της επιφάνειας $\Phi=K\cap S_{+}$ είναι:

$\displaystyle{ \Phi(r, \theta)= r \cos \theta \vec{i} + r \sin \theta \vec{j} + \sqrt{4 \rho^2 - r^2} \vec{k}, \qquad -\dfrac{\pi}{2} \leqslant \theta \leqslant \dfrac{\pi}{2}, \quad 0 \leqslant r \leqslant 2 \rho \cos \theta }$

Είναι $\displaystyle{ \dfrac{\partial \vec{\Phi}}{\partial r}(r,\theta)=\dfrac{\partial x}{\partial r}(r,\theta) \, \vec{i} + \dfrac{\partial y}{\partial r}(r,\theta) \, \vec{j} + \dfrac{\partial z}{\partial r}(r,\theta) \, \vec{k} =\cos \theta\, \vec{i} + \sin \theta \, \vec{j} - \dfrac{r}{\sqrt{4 \rho^2 - r^2}} \, \vec{k}, }$
και
$\displaystyle{ \dfrac{\partial \vec{\Phi}}{\partial \theta}(r,\theta)=\dfrac{\partial x}{\partial \theta}(r,\theta) \, \vec{i} + \dfrac{\partial y}{\partial \theta}(r,\theta) \, \vec{j} + \dfrac{\partial z}{\partial \theta}(r,\theta) \, \vec{k} =-r \sin \theta\, \vec{i} + r \cos \theta \, \vec{j} +0 \, \vec{k}. }$

$\displaystyle{ \vec{n}=\dfrac{\partial \vec{\Phi}}{\partial r}(r,\theta) \times \dfrac{\partial \vec{\Phi}}{\partial \theta}(r,\theta) = \det \begin{pmatrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} & \frac{\partial z}{\partial r}\\ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta} \end{pmatrix} = \det \begin{pmatrix} \vec{i} & \vec{j} & \vec{k} \\ \cos \theta & \sin \theta & -\dfrac{r}{\sqrt{4 \rho^2 - r^2}}\\ -r \sin \theta & r \cos \theta & 0 \end{pmatrix} }$

$\displaystyle{ = \dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{i} -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}} \, \vec{j} + r \, \vec{k} }$

{\color{blue} Θα δείξουμε ότι το διάνυσμα $\vec{n}$ βλέπει προς το εξωτερικό της επιφάνειας.

Όταν $x=\rho, \, y=0$ τότε απο την εξίσωση $x^2+y^2+z^2 = 4 \rho^2$ βρίσκουμε $z=\sqrt{3} \rho$ αφού z>0

.

Το σημείο $A(\rho, 0, \sqrt{3} \rho)$ του τμήματος της σφαίρας αντιστοιχεί για $r=\rho, \, \theta=0$ .
Δηλαδή, $(\rho, 0, \sqrt{3} \rho) = \Phi(\rho,0)$ .

$\vec{n}(\rho, 0)= \dfrac{\rho}{\sqrt{3}}\vec{i} + 0 \vec{j}+ \rho \vec{k}$ .

Παρατηρούμε ότι $\vec{n} \cdot \vec{k} = (\dfrac{\rho}{\sqrt{3}}\vec{i} + 0 \vec{j}+ \rho \vec{k}) \cdot (0,0,1)= \rho>0$ .

Δηλαδή τα διανύσματα $\vec{n}$ και $\vec{k}$ σχηματίζουν οξεία γωνία μεταξύ τους και επομένως το διάνυσμα $\vec{n}$ βλέπει προς τα έξω (του τμήματος) της σφαίρας.

Διαφορετικά: Το διάνυσμα θέσης του σημείου

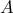του τμήματος της σφαίρας είναι $\overrightarrow{OA}= (\rho, 0, \sqrt{3} \rho)$ .

Τα διανύσματα $\overrightarrow{OA}, \, \vec{n}$ είναι παράλληλα και ομόρροπα.}

Άρα,

$\displaystyle{ \iint \limits_{K\cap S_{+}}{(z,x,y)\cdot\overline{n}\, d\sigma} =\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} (\sqrt{4 \rho^2 - r^2}, r \cos \theta, r \sin \theta) \cdot ( \dfrac{r^2 \cos \theta}{\sqrt{4 \rho^2 - r^2}}, -\dfrac{r^2 \sin \theta}{\sqrt{4 \rho^2 - r^2}}, + r) \, dr d \theta }$

$\displaystyle{ =\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{0}^{2 \rho \cos \theta} (r^2 \cos \theta -\dfrac{r^3 \cos \theta \sin \theta}{\sqrt{4 \rho^2 - r^2}} + r^2 \sin \theta) \, dr d \theta =\ldots = \rho^3 \pi. }$

ttheodoros · #14

Η λύση 2 όπου χρησιμοποίησα το Θεώρημα απόκλισης του Gauss έχει πρόβλημα..

Δεν ξέρω αν υπάρχει τρόπος "να σωθεί".

Διερωτούμαι πάντως πως βγαίνει το ίδιο αποτέλεσμα έστω και με διαφορετικό πρόσημο (αυτό μπορεί να οφείλεται σε αντίθετο προσανατολισμό της επιφάνειας).

#15

Για να χρησιμοποιήσουμε το θεώρημα αποκλίσεως πρέπει να έχουμε κλειστή επιφάνεια.

Η επιφάνεια που μας δίνεται δεν είναι κλειστή μπορούμε όμως να την κλείσουμε και μετά να χρησιμοποιήσουμε το θεώρημα αποκλίσεως ως εξής:

Γράφω $S_{top}$ για την δοσμένη επιφάνεια, $S_{cyl}$ για την κυλινδρική επιφάνεια που βρίσκεται μεταξύ της δοσμένης επιφάνειας και του επιπέδου z=0

, και $S_{bot}$ για το κάτω μέρος της κυλινδρικής επιφάνειας που βρίσκεται πάνω στο επίπεδο z=0

. (Θα δοθούν αργότερα και παραμετρικές εξισώσεις.)

Έστω $S = S_{top} \cup S_{cyl} \cup S_{bot}$ . Τότε μπορούμε να εφαρμόσουμε το θεώρημα αποκλίσεως για να πάρουμε

$\displaystyle \iint_S \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S = \iiint_V \nabla \cdot \mathbf{F} \, \mathrm{d}V = 0$

αφού $\nabla \cdot \mathbf{F} = 0$ .

Η επιφάνεια $S_{bot}$ έχει παραμετρική εξίσωση $(x,y,z) = (p+ r\cos{\vartheta},r\sin{\vartheta},0)$ όπου $0 \leqslant r \leqslant p$ και $0 \leqslant \vartheta \leqslant 2\pi$ .

Το εξωτερικό κάθετο διάνυσμα είναι προφανώς το $-\mathbf{k}$ και είναι γνωστό (ή υπολογίζεται με τον γνωστό τρόπο) ότι $\mathrm{d}S = r\,\mathrm{d}r\,\mathrm{d}\vartheta$ . Οπότε παίρνουμε:

$\displaystyle \iint_{S_{bot}} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S = -\int_0^{2\pi}\int_{0}^{p} r^2 \sin{\vartheta} \,\mathrm{d}r\,\mathrm{d}\vartheta = 0.$ (Ολοκληρώνουμε πρώτα ως προς $\vartheta$ .)

Η επιφάνεια $S_{cyl}$ έχει παραμετρική εξίσωση $(x,y,z) = (p+ p\cos{\vartheta},p\sin{\vartheta},z)$ όπου $0 \leqslant \vartheta \leqslant 2\pi$ και επιπλέον το

ικανοποιεί $z \geqslant 0$ και $x^2 + y^2 + z^2 \leqslant 4p^2$ . Μετά από κάποιες απλές πράξεις που παραλείπω, βγαίνει ότι $0 \leqslant z \leqslant 2p \sin{(\vartheta/2)}$ .

Το εξωτερικό κάθετο διάνυσμα είναι (γνωστό) το $\cos{\vartheta}\, \mathbf{i} + \sin{\vartheta}\, \mathbf{j}$ και έχουμε (πάλι γνωστό) $\mathrm{d}S = r\,\mathrm{d}z\,\mathrm{d}\vartheta$ . Οπότε παίρνουμε:

$\displaystyle \begin{aligned} \iint_{S_{cyl}} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S &= \int_0^{2\pi}\int_{0}^{2p\sin{(\vartheta/2)}} \left[pz \cos{\vartheta} + p^2\sin{\vartheta}(1+\cos{\vartheta})\right] \mathrm{d}z\,\mathrm{d}\vartheta \\ &= 2p^3\int_0^{2\pi} \left[\cos{\vartheta}\sin^2{(\vartheta/2)} + \sin{\vartheta}(1+\cos{\vartheta})\sin{(\vartheta/2)} \right] \mathrm{d}z\,\mathrm{d}\vartheta\\ &= \cdots = -p^3 \pi \end{aligned}$

Οπότε εν τέλει έχουμε

$\displaystyle \iint_{S_{top}} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S= \iint_{S} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S- \iint_{S_{bot}} \mathbf{F} \cdot \mathbf{n}\, \mathrm{d}S - \iint_{S_{cyl}} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S= p^3\pi$

Χρειάστηκε εδώ να υπολογίσουμε δύο άλλα ολοκληρώματα αλλά οι πράξεις είναι κάπως πιο απλές από τον υπολογισμό του ζητούμενου. Π.χ. η επιλογή των κάθετων διανυσμάτων είναι προφανής ενώ στο ζητούμενο χρειάζεται δουλειά.

Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Re: Ολοκλήρωμα πολυμεταβλητής συνάρτησης

Μέλη σε σύνδεση