Σελίδα 1 από 1
ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Τετ Ιούλ 04, 2018 6:44 pm
από v2gls
Θα ήθελα τη βοηθειά σας στο εξής ερώτημα :
Προσπαθώ να δω αν ισχύει ο ισχυρισμός : έστω μ μετρο πιθανότητας στο

. Υπάρχει ακολουθία μετρων πιθανότητας του

, η οποία αποτελείται από απολύτως συνεχής μέτρα ως προς το μέτρο Lebesgue και η οποία συγκλίνει ασθενώς στο μ ;
Γνωρίζει κάποιος πως θα βρω αυτή την ακολουθία ;
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Παρ Αύγ 31, 2018 4:49 pm
από v2gls
Αυτή είναι μια δική μου λύση. Κάθε γνώμη ή επισήμανση λάθους είναι ευπρόσδεκτη.

Έστω

μέτρο πιθανότητας στον

. Θα δείξουμε ότι υπάρχει

ακολουθία μέτρων πιθανότητας τέτοια ώστε

και

για f συνεχή συνάρτηση

.
απόδειξη
Έστω

ακολουθία συμμετρικών mollifiers.
(δηλαδή

.\\
Θέτουμε

.Και βλέπουμε ότι το

μέτρο πιθανότητας απολύτως συνεχές ως προς το μέτρο Lebesque.
Για τη τελευταία ιδιότητα : έστω f συνεχής



.
Θα χρησιμοποιήσουμε Θεώρημα Κυριαρχημένης Σύγκλισης για να δείξουμε ότι το τελευταίο ολοκλήρωμα συγκλίνει στο

.
Για την ακολουθία

έχουμε ότι

. Συνεπώς κάθε όρος της ακολουθίας είναι ολοκληρώσιμη συνάρτηση ως προς το μέτρο πιθανότητας

.
Έστω

. Θα δείξουμε ότι

συγκλίνει στο
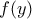
.
Έστω

.

.
Αλλά επειδή η f είναι συνεχής στο y έχουμε ότι

τέτοιο ώστε

με

τότε

.
Επιλέγουμε

τέτοιο ώστε
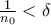
. Τότε για

και για χ

έχουμε ότι

. Έτσι από την

έχουμε ότι

. Έτσι

. \\
Συνεπώς

.
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Παρ Αύγ 31, 2018 10:34 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
v2gls έγραψε: ↑Παρ Αύγ 31, 2018 4:49 pm
Αυτή είναι μια δική μου λύση. Κάθε γνώμη ή επισήμανση λάθους είναι ευπρόσδεκτη.

Έστω

μέτρο πιθανότητας στον

. Θα δείξουμε ότι υπάρχει

ακολουθία μέτρων πιθανότητας τέτοια ώστε

και

για f συνεχή συνάρτηση

.
απόδειξη
Έστω

ακολουθία συμμετρικών mollifiers.
(δηλαδή

.\\
Θέτουμε

.Και βλέπουμε ότι το

μέτρο πιθανότητας απολύτως συνεχές ως προς το μέτρο Lebesque.
Για τη τελευταία ιδιότητα : έστω f συνεχής



.
Θα χρησιμοποιήσουμε Θεώρημα Κυριαρχημένης Σύγκλισης για να δείξουμε ότι το τελευταίο ολοκλήρωμα συγκλίνει στο

.
Για την ακολουθία

έχουμε ότι

. Συνεπώς κάθε όρος της ακολουθίας είναι ολοκληρώσιμη συνάρτηση ως προς το μέτρο πιθανότητας

.
Έστω

. Θα δείξουμε ότι

συγκλίνει στο
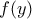
.
Έστω

.

.
Αλλά επειδή η f είναι συνεχής στο y έχουμε ότι

τέτοιο ώστε

με

τότε

.
Επιλέγουμε

τέτοιο ώστε
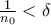
. Τότε για

και για χ

έχουμε ότι

. Έτσι από την

έχουμε ότι

. Έτσι

. \\
Συνεπώς

.
Η ιδέα της απόδειξης είναι σωστή.
Υπάρχει ένα πρόβλημα γιατί χρησιμοποιείς ότι η συνάρτηση είναι ομοιόμορφα συνεχής.
Δεν είναι λάθος γιατί η συνεχής συνάρτηση είναι ειδικού τύπου.
Αν δεν κάνω λάθος μπορούμε να την πάρουμε με συμπαγή φορέα οπότε είναι ομοιόμορφα συνεχής.
Μπορείς να δουλέψεις και διαφορετικά.
Το αρχικό μέτρο έχει μάζα μικρή έξω από ένα συμπαγές που μπορείς να θεωρήσεις ότι είναι κύβος.
Τον κύβο των χωρίζεις σε μικρούς κύβους.
Η συνάρτηση πυκνότητας την βάζεις σταθερή σε κάθε μικρό κύβο έτσι ώστε το ολοκλήρωμα της πάνω σε αυτόν
να είναι ίσο με το μέτρο του.κλπ
Τεχνικά είναι πολύ πιο δύσκολο από το δικό σου αλλά δίνει καλύτερη εικόνα για τα μέτρα.
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Σάβ Σεπ 01, 2018 2:08 pm
από v2gls
Σας ευχαριστώ. Πράγματι χρησιμοποιώ ομοιόμορφη συνέχεια. Δε το είχα προσέξει.
Τι εννοείτε "ειδικού τύπου";
Επίσης, αν πάρω την f να έχει συμπαγή φορέα (που τότε πράγματι δουλεύουν όλα) μετά μπορώ να επεκτείνω σε συνεχείς συναρτήσεις ;
Γενικά νομίζω ότι για συναρτήσεις ορισμένες στον

δε μπορώ να προσεγγίσω τις συνεχείς από συνεχείς με συμπαγή φορέα. Οπότε μήπως τελικά αυτό που θέλω αρχικά να δείξω δεν ισχύει για συναρτήσεις του

που είναι μόνο συνεχείς;
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Σάβ Σεπ 01, 2018 6:05 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
v2gls έγραψε: ↑Σάβ Σεπ 01, 2018 2:08 pm
Σας ευχαριστώ. Πράγματι χρησιμοποιώ ομοιόμορφη συνέχεια. Δε το είχα προσέξει.
Τι εννοείτε "ειδικού τύπου";
Επίσης, αν πάρω την f να έχει συμπαγή φορέα (που τότε πράγματι δουλεύουν όλα) μετά μπορώ να επεκτείνω σε συνεχείς συναρτήσεις ;
Γενικά νομίζω ότι για συναρτήσεις ορισμένες στον

δε μπορώ να προσεγγίσω τις συνεχείς από συνεχείς με συμπαγή φορέα. Οπότε μήπως τελικά αυτό που θέλω αρχικά να δείξω δεν ισχύει για συναρτήσεις του

που είναι μόνο συνεχείς;
Για την ασθενή σύγκλιση πρέπει να πάρεις συνεχείς με συμπαγή φορέα.
Εισαι εντάξει λοιπόν.
Για να εξετάσουμε ασθενή σύγκλιση στοιχείων πρέπει να βρούμε ένα χώρο με νόρμα που τα στοιχεία που
εξετάζουμε να είναι στον δυικό του.
Ο δυικός των συνεχών με συμπαγή φορέα σε ένα τοπικά συμπαγή χώρο είναι τα μέτρα κλπ.
Για να διαπυστώσεις ότι δεν κάνουν οι συνεχείς σκέψου τι νόρμα θα έβαζες;
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Κυρ Σεπ 02, 2018 10:00 pm
από v2gls
Μπερδεύτηκα. Από το θεώρημα Portmanteau για χαρακτηρισμό της ασθενούς σύγκλισης μέτρων πιθανότητας πρέπει να θεωρήσω συνεχή και φραγμένη συνάρτηση για να δείξω ασθενή σύγκλιση (όχι;). (όπου η ιδιότητα φραγμένη δε φαίνεται χρήσιμη στη παραπάνω απόδειξη)
Η απόδειξη ναι μεν δουλεύει αν η f έχει και συμπαγή φορέα αλλά αυτό γιατί δίνει ασθενή σύγκλιση ;
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Δευ Σεπ 03, 2018 12:18 am
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
v2gls έγραψε: ↑Κυρ Σεπ 02, 2018 10:00 pm
Μπερδεύτηκα. Από το θεώρημα Portmanteau για χαρακτηρισμό της ασθενούς σύγκλισης μέτρων πιθανότητας πρέπει να θεωρήσω συνεχή και φραγμένη συνάρτηση για να δείξω ασθενή σύγκλιση (όχι;). (όπου η ιδιότητα φραγμένη δε φαίνεται χρήσιμη στη παραπάνω απόδειξη)
Η απόδειξη ναι μεν δουλεύει αν η f έχει και συμπαγή φορέα αλλά αυτό γιατί δίνει ασθενή σύγκλιση ;
Κοίταξε τι λέει το θεώρημα του Portmanteau στο
http://theanalysisofdata.com/probability/8_5.html
Λέει ακριβώς ότι μπορούμε να πάρουμε τις συνεχείς με συμπαγή φορέα.
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Δευ Σεπ 03, 2018 11:47 am
από v2gls
Πράγματι. Δεν είχα ξαναδεί την ισοδυναμία με χρήση συναρτήσεων με συμπαγή φορέα στο Portmanteau.
Σας ευχαριστώ !
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Τρί Φεβ 05, 2019 10:30 pm
από v2gls
Σαν συνέχεια του παραπάνω ερωτήματος θέλω να δείξω το εξής :
Θεωρούμε την ακολουθία

όπως ορίστηκε παραπάνω.
Έστω

συνεχής,

, με

και

(ίσως αυτές οι δύο ιδιότητες δε χρειάζονται για το ερώτημα)
(παράδειγμα συνάρτησης που ικανοποιεί τις ιδιότητες αυτές είναι η

όπου

)
Ισχύει ότι

;
Αν δεν ισχύει το παραπάνω αποτέλεσμα, μπορώ να πάρω το ασθενέστερο

;
Re: ερώτημα θεωρίας μέτρου
Δημοσιεύτηκε: Πέμ Φεβ 07, 2019 2:23 pm
από v2gls
Μέχρι στιγμής μπορώ να κάνω το εξής :
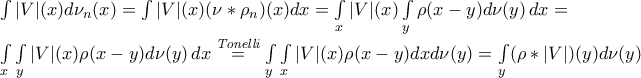
.
Δε ξέρω πως να συνεχίσω όμως.
 . Υπάρχει ακολουθία μετρων πιθανότητας του
. Υπάρχει ακολουθία μετρων πιθανότητας του  , η οποία αποτελείται από απολύτως συνεχής μέτρα ως προς το μέτρο Lebesgue και η οποία συγκλίνει ασθενώς στο μ ;
, η οποία αποτελείται από απολύτως συνεχής μέτρα ως προς το μέτρο Lebesgue και η οποία συγκλίνει ασθενώς στο μ ; . Υπάρχει ακολουθία μετρων πιθανότητας του
. Υπάρχει ακολουθία μετρων πιθανότητας του  , η οποία αποτελείται από απολύτως συνεχής μέτρα ως προς το μέτρο Lebesgue και η οποία συγκλίνει ασθενώς στο μ ;
, η οποία αποτελείται από απολύτως συνεχής μέτρα ως προς το μέτρο Lebesgue και η οποία συγκλίνει ασθενώς στο μ ; μέτρο πιθανότητας στον
μέτρο πιθανότητας στον  . Θα δείξουμε ότι υπάρχει
. Θα δείξουμε ότι υπάρχει  ακολουθία μέτρων πιθανότητας τέτοια ώστε
ακολουθία μέτρων πιθανότητας τέτοια ώστε  και
και  για f συνεχή συνάρτηση
για f συνεχή συνάρτηση  ακολουθία συμμετρικών mollifiers.
ακολουθία συμμετρικών mollifiers. .\\
.\\ .Και βλέπουμε ότι το
.Και βλέπουμε ότι το  μέτρο πιθανότητας απολύτως συνεχές ως προς το μέτρο Lebesque.
μέτρο πιθανότητας απολύτως συνεχές ως προς το μέτρο Lebesque.

 .
. .
. έχουμε ότι
έχουμε ότι  . Συνεπώς κάθε όρος της ακολουθίας είναι ολοκληρώσιμη συνάρτηση ως προς το μέτρο πιθανότητας
. Συνεπώς κάθε όρος της ακολουθίας είναι ολοκληρώσιμη συνάρτηση ως προς το μέτρο πιθανότητας  . Θα δείξουμε ότι
. Θα δείξουμε ότι  συγκλίνει στο
συγκλίνει στο 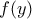 .
. .
.  .
.  τέτοιο ώστε
τέτοιο ώστε με
με τότε
τότε  .
.  τέτοιο ώστε
τέτοιο ώστε 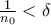 . Τότε για
. Τότε για  και για χ
και για χ έχουμε ότι
έχουμε ότι  . Έτσι από την
. Έτσι από την  έχουμε ότι
έχουμε ότι  . Έτσι
. Έτσι  . \\
. \\ .
. όπως ορίστηκε παραπάνω.
όπως ορίστηκε παραπάνω. συνεχής,
συνεχής,  , με
, με και
και  (ίσως αυτές οι δύο ιδιότητες δε χρειάζονται για το ερώτημα)
(ίσως αυτές οι δύο ιδιότητες δε χρειάζονται για το ερώτημα) όπου
όπου  )
)  ;
; ;
;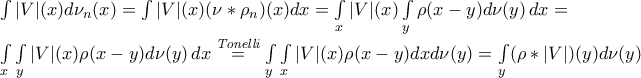 .
.