Σελίδα 1 από 1
Τοπικά και ολικά ακρότατα
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 6:58 pm
από Tolaso J Kos
Έστω

όπου

και

ο μοναδιαίος κύκλος κέντρου

. Βρείτε τα τοπικά και ολικά ακρότατα της

.
Από σημερινή εξέταση Απ. ΙΙΙ σε κάποιο μαθηματικό τμήμα.
Re: Τοπικά και ολικά ακρότατα
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 8:24 pm
από grigkost


ο μοναδιαίος κύκλος με κέντρο το

. Η εικόνα

είναι η καμπύλη που είναι η τομή της επιφάνειας

με τον κύλινδρο

. Θέτοντας

από τις παραπάνω σχέσεις

, προκύπτει ότι μια παραμετρική παράσταση της

είναι

Η μεγαλύτερη και η μικρότερη τιμή της

-συνιστώσας είναι η
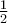
και

, αντίστοιχα και προκύπτουν για

και

, αντίστοιχα.
Επομένως η συνάρτηση

παρουσιάζει ολικό μέγιστο στα σημεία

,

κι ολικό ελάχιστο στα σημεία

,

.
Από την μονοτονία της

προκύπτει ότι δεν υπάρχουν άλλα (τοπικά) ακρότατα.

- min-max_f.png (48.07 KiB) Προβλήθηκε 883 φορές
Παρατήρηση: Προφανώς υπάρχει κι άλλος (κλασικός) τρόπος επίλυσης.
Re: Τοπικά και ολικά ακρότατα
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 10:45 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Tolaso J Kos έγραψε: ↑Τρί Ιουν 12, 2018 6:58 pm
Έστω

όπου

και

ο μοναδιαίος κύκλος κέντρου

. Βρείτε τα τοπικά και ολικά ακρότατα της

.
Από σημερινή εξέταση Απ. ΙΙΙ σε κάποιο μαθηματικό τμήμα.
Από ότι γνωρίζω με

συμβολίζουμε τον μοναδιαίο δίσκο.
Δηλαδή

Τον μοναδιαίο κύκλο συνήθως τον συμβολίζουμε με

.
Τόλη το θέμα πως ακριβώς είναι;
Re: Τοπικά και ολικά ακρότατα
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 10:56 pm
από Tolaso J Kos
Σταύρο,
το θέμα είναι ακριβώς όπως ανέβηκε. Βέβαια ο διδάσκων έχει γράψει

για το κύκλο αλλά επειδή εγώ χρησιμοποιώ και για το δίσκο και για το κύκλο

το έδωσα έτσι. Εφόσον όμως έχω δώσει τι είναι το

στη συγκεκριμένη άσκηση , δε νομίζω να υπάρχει θέμα παρερμηνείας.
Re: Τοπικά και ολικά ακρότατα
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 11:09 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Αφού ξέρουμε πως ήταν το θέμα να γράψω μια στοιχειώδη λύση.
Θέλουμε μέγιστο ελάχιστο του

όταν

.
Ειναι

Οπου η αριστερή ισότητα πιάνεται όταν
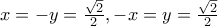
και η δεξιά όταν

.
Αρα η μέγιστη τιμή είναι
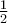
και πιάνεται στα

και η ελάχιστη τιμή είναι

και πιάνεται στα

 όπου
όπου  και
και  ο μοναδιαίος κύκλος κέντρου
ο μοναδιαίος κύκλος κέντρου  . Βρείτε τα τοπικά και ολικά ακρότατα της
. Βρείτε τα τοπικά και ολικά ακρότατα της  .
.  όπου
όπου  και
και  ο μοναδιαίος κύκλος κέντρου
ο μοναδιαίος κύκλος κέντρου  . Βρείτε τα τοπικά και ολικά ακρότατα της
. Βρείτε τα τοπικά και ολικά ακρότατα της  .
. 
 ο μοναδιαίος κύκλος με κέντρο το
ο μοναδιαίος κύκλος με κέντρο το  . Η εικόνα
. Η εικόνα  είναι η καμπύλη που είναι η τομή της επιφάνειας
είναι η καμπύλη που είναι η τομή της επιφάνειας  με τον κύλινδρο
με τον κύλινδρο  . Θέτοντας
. Θέτοντας 
 , προκύπτει ότι μια παραμετρική παράσταση της
, προκύπτει ότι μια παραμετρική παράσταση της 
 -συνιστώσας είναι η
-συνιστώσας είναι η 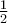 και
και  , αντίστοιχα και προκύπτουν για
, αντίστοιχα και προκύπτουν για  και
και  , αντίστοιχα.
, αντίστοιχα.  ,
,  κι ολικό ελάχιστο στα σημεία
κι ολικό ελάχιστο στα σημεία  ,
,  .
. προκύπτει ότι δεν υπάρχουν άλλα (τοπικά) ακρότατα.
προκύπτει ότι δεν υπάρχουν άλλα (τοπικά) ακρότατα. συμβολίζουμε τον μοναδιαίο δίσκο.
συμβολίζουμε τον μοναδιαίο δίσκο.
 .
. το έδωσα έτσι. Εφόσον όμως έχω δώσει τι είναι το
το έδωσα έτσι. Εφόσον όμως έχω δώσει τι είναι το 
 .
.
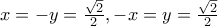
 .
.
