Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

dimitris0101 · #1

Καλησπέρα ,
Λύνω μια άσκηση η οποία σε ένα ερώτημα ζητά <<Βρείτε το μοναδιαίο διάνυσμα στην κατεύθυνση του οποίου ο ρυθμός μεταβολής των τιμών της f στο σημείο (1,1) είναι ο μέγιστος δυνατός >>. Έχω βρεί τον ζητούμενο ρυθμό μεταβολής αλλά δεν μπορώ να καταλάβω πως βρίσκω το μοναδιαίο διάνυσμα που ζητείται και πως αξιοποιώ την απαίτηση του <<μέγιστου δυνατού>> .
Ευχαριστώ εκ των προτέρων .

Λάμπρος Κατσάπας · #2

dimitris0101 έγραψε: ↑
Κυρ Ιουν 10, 2018 9:22 pm
Καλησπέρα ,
Λύνω μια άσκηση η οποία σε ένα ερώτημα ζητά <<Βρείτε το μοναδιαίο διάνυσμα στην κατεύθυνση του οποίου ο ρυθμός μεταβολής των τιμών της f στο σημείο (1,1) είναι ο μέγιστος δυνατός >>. Έχω βρεί τον ζητούμενο ρυθμό μεταβολής αλλά δεν μπορώ να καταλάβω πως βρίσκω το μοναδιαίο διάνυσμα που ζητείται και πως αξιοποιώ την απαίτηση του <<μέγιστου δυνατού>> .
Ευχαριστώ εκ των προτέρων .

Υπόδειξη: Αν $\vec{a}\neq \vec{0}$ το $\frac{\vec{a}}{\left \| \vec{a} \right \|}$ είναι μοναδιαίο.

#3

dimitris0101 έγραψε: ↑
Κυρ Ιουν 10, 2018 9:22 pm
Καλησπέρα ,
Λύνω μια άσκηση η οποία σε ένα ερώτημα ζητά <<Βρείτε το μοναδιαίο διάνυσμα στην κατεύθυνση του οποίου ο ρυθμός μεταβολής των τιμών της f στο σημείο (1,1) είναι ο μέγιστος δυνατός >>. Έχω βρεί τον ζητούμενο ρυθμό μεταβολής αλλά δεν μπορώ να καταλάβω πως βρίσκω το μοναδιαίο διάνυσμα που ζητείται και πως αξιοποιώ την απαίτηση του <<μέγιστου δυνατού>> .
Ευχαριστώ εκ των προτέρων .

Αυτή είναι μια γνωστή πρόταση: Ο μέγιστος δυνατός ρυθμός μεταβολής των τιμών μιας πραγματικής συνάρτησης

διανυσματικής μεταβλητής 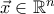$\vec{x}\in\mathbb{R}^n$ στο τυχόν σημείο $\vec{x}_0$ επιτυγχάνεται στην διεύθυνση $({\rm{grad}}\,f)(\vec{x}_0)$ . ( Για να είναι μοναδιαίο αρκεί να διαιρέσουμε με το μέτρο του, εφ' όσον $({\rm{grad}}\,f)(\vec{x}_0)\neq\vec{0}$ ).

dimitris0101 · #4

Άρα ουσιαστικά βρίσκω το μοναδιαίο διάνυσμα της παραγώγου της f στο σημείο που μου δίνεται . Και εάν μου ζητείται ο ελάχιστος δυνατός ρυθμός μεταβολής της συνάρτησης σε ένα σημείο , είναι το μοναδίαιο διάνυσμα του αντίθετου διανύσματος της παραγώγου της f στο σημείο αυτό. Σωστός ;

#5

dimitris0101 έγραψε: ↑
Δευ Ιουν 11, 2018 1:17 am
Άρα ουσιαστικά βρίσκω το μοναδιαίο διάνυσμα της παραγώγου της f στο σημείο που μου δίνεται . Και εάν μου ζητείται ο ελάχιστος δυνατός ρυθμός μεταβολής της συνάρτησης σε ένα σημείο , είναι το μοναδίαιο διάνυσμα του αντίθετου διανύσματος της παραγώγου της f στο σημείο αυτό. Σωστός ;

"... ο ελάχιστος δυνατός ρυθμός μεταβολής της συνάρτησης σε ένα σημείο, είναι στην διεύθυνση του αντίθετου διανύσματος της παραγώγου της

στο σημείο αυτό..."

Ναι. Αφού για $({\rm{grad}}f)(\vec{x})\neq\vec{0}$ , ο ρυθμός μεταβολής της

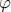στο σημείο $\vec{x}$ και στην διεύθυνση του μοναδιαίου $\vec{u}$ ισούται με ${\bf{D}}_{\vec{u}}f(\vec{x})=\|({\rm{grad}}f)(\vec{x})\|\cos\varphi$ , όπου $\varphi$ η γωνία που σχηματίζουν τα $({\rm{grad}}f)(\vec{x})$ και $\vec{u}$ .

Παρατήρηση: Αν $({\rm{grad}}f)(\vec{x})=\vec{0}$ , τότε το παραπάνω δεν ισχύει πάντοτε. Σε αυτήν την περίπτωση το $\vec{x}$ είναι ένα κρίσιμο σημείο της

και πρέπει να μελετήσουμε τον ρυθμό μεταβολής στις διάφορες διευθύνσεις.

Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

Re: Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

Re: Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

Re: Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

Re: Ρυθμός μεταβολής σε συνάρτηση δύο μεταβλητών

Μέλη σε σύνδεση