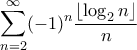
Σειρά με ακέραιο μέρος
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Ας αποδείξουμε την "αγελάδα" ....
Έχουμε:

Υπάρχουν ακόμα πολλές αποδείξεις για αυτή τη σειρά... και φυσικά πολλές γενικεύσεις. Θα δώσω κάποιες όταν γυρίσω από το μάθημα.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Αφού δόθηκε λύση να "αποκαλύψουμε" ότι η συγκεκριμένη σειρά οφείλεται στον Giovanni Vacca και, για αυτό φέρει το όνομά του.Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 11:10 am...Υπάρχουν ακόμα πολλές αποδείξεις για αυτή τη σειρά...
Τόλη, καλό θα ήταν να δούμε και μια-δυο άλλες αποδείξεις. (Αν και αυτή που έδωσες, νομίζω ότι είναι η κλασσικότερη).

- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Στο paper υπάρχει μία ακόμα απόδειξη με γεννήτριες.
Στηρίζεται στον υπολογισμό του ολοκληρώματος όπου
όπου  .
.
Την απόδειξη της παραπάνω ισότητας την έχω ανεβάσει στο blog μου.


Στηρίζεται στον υπολογισμό του ολοκληρώματος
 όπου
όπου  .
.Την απόδειξη της παραπάνω ισότητας την έχω ανεβάσει στο blog μου.
Γρηγόρη αυτός είναι και ο λόγος που έγραψα στην απάντηση "αγελάδα" αφού στα Ισπανικά vaca ( la ) είναι η αγελάδα..grigkost έγραψε: ↑Σάβ Ιουν 02, 2018 11:26 am
Αφού δόθηκε λύση να "αποκαλύψουμε" ότι η συγκεκριμένη σειρά οφείλεται στον Giovanni Vacca και, για αυτό φέρει το όνομά του.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Ευχαριστούμε Τόλη.Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 12:37 pmΣτο paper υπάρχει μία ακόμα απόδειξη με γεννήτριες.
Ευτυχώς...που ο συγκεκριμένος Vacca ήταν Ιταλός!Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 12:37 pm... "αγελάδα" αφού στα Ισπανικά vaca ( la ) είναι η αγελάδα..


Re: Σειρά με ακέραιο μέρος
Τι δουλειά έχουν τα Ισπανικά βρε Τόλη; Ιταλός ο τύπος και vacca είναι η αγελάδα στα ιταλικά (με δύο c!). Porca vacca!
Ευχαριστώ και τους δυο σας, γηράσκω αεί διδασκόμενος.

Ευχαριστώ και τους δυο σας, γηράσκω αεί διδασκόμενος.
Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Δημήτρη,
ιταλικά δε ξέρω .. Μόνο Ισπανικά, Αγγλικά και Γερμανικά. Οπότε έκανα τη σύνδεση του ονόματος με τα Ισπανικά.. !!
grigkost έγραψε: ↑Σάβ Ιουν 02, 2018 12:44 pmΕυτυχώς...που ο συγκεκριμένος Vacca ήταν Ιταλός!Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 12:37 pm... "αγελάδα" αφού στα Ισπανικά vaca ( la ) είναι η αγελάδα..

Η φαντασία είναι σημαντικότερη από τη γνώση !


- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Από τα παραπάνω εύκολα συμπεραίνουμε ότι ...Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 12:54 pm.... "αγελάδα" αφού στα Ισπανικά vaca ( la ) είναι η αγελάδα..
 grigkost έγραψε: ↑Σάβ Ιουν 02, 2018 12:44 pmΕυτυχώς...που ο συγκεκριμένος Vacca ήταν Ιταλός!Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 12:37 pm... "αγελάδα" αφού στα Ισπανικά vaca ( la ) είναι η αγελάδα..
grigkost έγραψε: ↑Σάβ Ιουν 02, 2018 12:44 pmΕυτυχώς...που ο συγκεκριμένος Vacca ήταν Ιταλός!Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 12:37 pm... "αγελάδα" αφού στα Ισπανικά vaca ( la ) είναι η αγελάδα..





- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Ας δούμε μερικά εξαιρετικά αποτελέσματα. Δεν έχω αποδείξεις για πολλά από αυτά.
1ο αποτέλεσμα:
Το συγκεκριμένο αποτέλεσμα οφείλεται στον A.W.Addison ο οποίος χρησιμοποίησε μία ολοκληρωτική αναπαράσταση της για να φτάσει στο εξής αποτέλεσμα:
για να φτάσει στο εξής αποτέλεσμα:

Γενίκευση: Έστω με
με 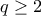 . Θεωρούμε το πολυώνυμο
. Θεωρούμε το πολυώνυμο  βαθμού
βαθμού  με τύπο:
με τύπο:
 Τότε:
Τότε:

Σημειώσατε πως καθώς το αυξάνει η σειρά συγκλίνει πιο γρήγορα.
αυξάνει η σειρά συγκλίνει πιο γρήγορα.
2o αποτέλεσμα:
Ισχύει ότι:
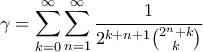
3ο αποτέλεσμα:
Το παρακάτω αποτέλεσμα οφείλεται στον Gosper.

1ο αποτέλεσμα:
Το συγκεκριμένο αποτέλεσμα οφείλεται στον A.W.Addison ο οποίος χρησιμοποίησε μία ολοκληρωτική αναπαράσταση της
 για να φτάσει στο εξής αποτέλεσμα:
για να φτάσει στο εξής αποτέλεσμα:
Γενίκευση: Έστω
 με
με 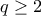 . Θεωρούμε το πολυώνυμο
. Θεωρούμε το πολυώνυμο  βαθμού
βαθμού  με τύπο:
με τύπο: Τότε:
Τότε:
Σημειώσατε πως καθώς το
 αυξάνει η σειρά συγκλίνει πιο γρήγορα.
αυξάνει η σειρά συγκλίνει πιο γρήγορα. 2o αποτέλεσμα:
Ισχύει ότι:
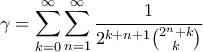
3ο αποτέλεσμα:
Το παρακάτω αποτέλεσμα οφείλεται στον Gosper.

Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Για να γυρίσουμε πίσω στην αρχική ερώτηση: Πώς θα αποδείκνυε κάποιος τη σύγκλιση ; Ωραία κάναμε τον υπολογισμό είδαμε πόσο κάνει; Για τη σύγκλιση ; Δε τη βλέπω να είναι προφανής !
Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Σειρά με ακέραιο μέρος
ΙσχύειTolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 7:29 pm
Για να γυρίσουμε πίσω στην αρχική ερώτηση: Πώς θα αποδείκνυε κάποιος τη σύγκλιση ; Ωραία κάναμε τον υπολογισμό είδαμε πόσο κάνει; Για τη σύγκλιση ; Δε τη βλέπω να είναι προφανής !
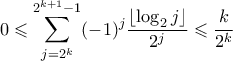 (ο πρώτος όρος του αθροίσματος, οι υπόλοιποι τον ελαττώνουν δύο-δύο), που συγκλίνει.
(ο πρώτος όρος του αθροίσματος, οι υπόλοιποι τον ελαττώνουν δύο-δύο), που συγκλίνει. Το γεγονός ότι η απόλυτη τιμή της ακολουθίας είναι γνησίως φθίνουσα σε κάθε διάστημα
![[2^k, 2^{k+1}-1] [2^k, 2^{k+1}-1]](/forum/ext/geomar/texintegr/latexrender/pictures/180c4aa27748e3370441e00c9cbac1e0.png) με εναλλασσόμενο πρόσημο σημαίνει ότι κάθε άθροισμα της μορφής
με εναλλασσόμενο πρόσημο σημαίνει ότι κάθε άθροισμα της μορφής  είναι απολύτως μικρότερο από ένα άθροισμα της μορφής
είναι απολύτως μικρότερο από ένα άθροισμα της μορφής  (μετακινούμε κατάλληλα τα άκρα του αθροίσματος), οπότε από το κριτήριο του Cauchy έπεται η σύγκλιση.
(μετακινούμε κατάλληλα τα άκρα του αθροίσματος), οπότε από το κριτήριο του Cauchy έπεται η σύγκλιση.Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά με ακέραιο μέρος
Μία άλλη ταυτότητα είναι η ακόλουθη ( εμφανίστηκε κατά τον υπολογισμό της αρχικής σειράς ) :

η οποία είναι πάρα πολύ εύκολη να αποδειχθεί.
Το εντυπωσιακό όμως με την ταυτότητα αυτή είναι ότι o Vacca την απέδειξε γεωμετρικά. Δε ξέρω τι ακριβώς έχει κάνει και θα ήθελα αν κάποιος μπορεί να βρει το συγκεκριμένο paper να το ανεβάσει. H ταυτότητα επιδέχεται και αναλυτική προσέγγιση την οποία έχουν ήδη κάνει ο Glaisher και ο Hardy.
Και τέλος μία πάρα πολύ γνωστή ισότητα είναι η ακόλουθη:


η οποία είναι πάρα πολύ εύκολη να αποδειχθεί.
Το εντυπωσιακό όμως με την ταυτότητα αυτή είναι ότι o Vacca την απέδειξε γεωμετρικά. Δε ξέρω τι ακριβώς έχει κάνει και θα ήθελα αν κάποιος μπορεί να βρει το συγκεκριμένο paper να το ανεβάσει. H ταυτότητα επιδέχεται και αναλυτική προσέγγιση την οποία έχουν ήδη κάνει ο Glaisher και ο Hardy.
Και τέλος μία πάρα πολύ γνωστή ισότητα είναι η ακόλουθη:

Η φαντασία είναι σημαντικότερη από τη γνώση !


-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Σειρά με ακέραιο μέρος
Το κομμάτι αυτό έχει πρόβλημα.Tolaso J Kos έγραψε: ↑Σάβ Ιουν 02, 2018 11:10 am
Ας αποδείξουμε την "αγελάδα" ....
Έχουμε:

Υπάρχουν ακόμα πολλές αποδείξεις για αυτή τη σειρά... και φυσικά πολλές γενικεύσεις. Θα δώσω κάποιες όταν γυρίσω από το μάθημα.

Ο σημαντικότερος λόγος είναι ότι δεν είναι

Θα πρότεινα να γραφεί

οπότε παίρνοντας όριο έχουμε το ζητούμενο.
Να σημειώσω ότι το πρώτο
 είναι από τον ορισμό του
είναι από τον ορισμό του  ενώ το δεύτερο θέλει ελάχιστη δουλίτσα.
ενώ το δεύτερο θέλει ελάχιστη δουλίτσα.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
